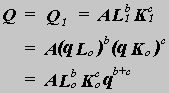43 Kysynnän
kasvu ja työllisyys Suomessa [ccc]
o Tuotannon määritelmä
o Tuotantofunktion muoto
o Alenevan rajatuotoksen
laki
o Rationaalisen
valinnan prosessi
o Työpanoksen kysyntä
1 Tuotantofunktiosta
työvoimantarvefunktioon
o 1
Alenevan rajatuotoksen laki
o 2 Suurtuotannon edut
2 Työpanoksen
ja pääomapanoksen suhde
o rajakorvaussuhde,
3 Työvoimantarvefunktion
joustot
o 1 Lyhyt tähtäys
o 2 Pitkä tähtäys
o 3 Laskelmia joustoilla
4 Työvoiman tarjonta
Tietokoneohjelmat: Kokeile
TreGraf o Kokeile
Employ
Taulukot: Työikäinen väestö
o Työvoiman tarjonta
Kuviot: Työllistetty työvoima
o Pääomakanta o
Työttömyys
Mielipide: RydmanKari-HeSa-19980218-Muutosvastarinta
Piirrokset: Palvelukseen
halutaan o Muurahaiset
o Työpanosen
joustot o Yksi
vielä o Labyrintti
(Hannu Kalla)
Derivaatta o Jousto
Makroteorian perusteet o Kansantalouden
kurssit o AJK kotisivu
Tuotanto
on tuotannontekijöiden yhdistämistä. Työpanos
ja pääomapanos ovat tietyn tuotannonmäärän aikaansaamiseksi
osaksi korvattavissa toisillaan. Tuotantopanosten keskinäinen korvattavuus
Cobb-Douglas tuotantofunktio
Mutta miksi juuri tämä potenssimuotoinen
funktio?
Onko sille olemassa jotakin erityisiä perusteluita? |
Huomio on kiinnitettävä tuotantofunktion derivaattaan.
- työpanoksen ja
- pääoma-panoksen rajatuotokset.
- Lineaarisen funktion (osittais)derivaattoja ovat funktion
kertoimet, siis vakiot.
- potenssimuotoisessa funktiossa derivaatta arvo riippuu
funktion arvosta
- työpanoksen ja pääomatuotoksen rajatuotokset
riippuvat käytettyjen työpanosten ja pääomapanosten
määristä.
Miksi on järkevää olettaa, että
työpanoksen rajatuotos ja
pääomapanoksen rajatuotos riippuvat tuotannon tasosta? |
alenevan rajatuotoksen
laki (ARL).
|
Alenevan rajatuotoksen
laki:
|
| Jos yhtä tuotannontekijäpanosta lisätään
tuotannossa, mutta muiden käyttö pidetään ennallaan,
alkaa lisäpanosyksikön antama tuotoksen lisäys ennen pitkää
alentua. |
Rationaalisen
valinnan prosessi
Miksi ARL vallitsee?
Siksi, että ihminen on järkevä ja tekee
taloudelliset valintansa rationaalisesti eli on sitä mieltä,
että enemmän on parempi kuin vähemmän.
Miten voimme olla varmoja,
että tuotantoprosessissa käyttäydytään rationaalisesti?
- ilmoituksella mahdollisimman monta hakijaa
- testein valitsemaan paras.
Tämä takaa, että työvoimaa palkataan paremmuusjärjestyksessä.
- viimeksi toimeen otettu on paras saatavissa oleva.
- jos jouduttaisiin ottamaan vielä yksi, se olisi
hiukan heikompi kuin edellinen
- työpanoksen rajatuotos alenisi
- samoin käy pääomapanokselle, sillä
ennen koneen hankintaa
- vertailevia investointilaskelmia
- vaihtoehtojen joukosta kannattavin
- suurimman rajatuotoksen antava.
Näin tapahtuu periaatteessa jokaisessa yrityksessä.
- Kilpailu pakottaa
kiinnittämään huomiota tuotantopanosten rajatuotoksiin.
- Koko kansantaloudessa vallitsee alenevan rajatuotoksen
laki, jos (edes melkein) kaikki toimivat rationaalisesti omalla kohdallaan.
- Alenevan rajatuotoksen laki onkin markkinatalouden keskeinen
salaisuus.
- Niin kauan kuin kilpailu vallitsee, niin kauan on taattu,
että myös rationaalisen valinnan prosessi toimii ja alenevan
rajatuotoksen laki ohjaa taloudellista päätöksentekoa.
Työpanoksen kysyntä
Mutta entä työvoimamarkkinat? Tässähän
on puhe
tuotannosta, joka tosin riippuu työpanoksesta. |
- emme voi tuotantofunktiokäsitettä lainkaan
käyttää sellaisenaan kansantalouden mallissa
- siinä jo tuotannon suuruus yhden kerran määräytyy
- lähtökohta kysynnän ja tarjonnan tasapainoehto:
bruttokansantuotos = bruttokansantuotoksen käyttö,
siis
- tarjonta (kokonaistuotanto)
= kysyntä. Tuotanto siis määräytyy jo
- Muodostetaan
työvoimantarvefunktio,
jossa tarvittava työpanos ilmaistaan kysynnästä
riippuvan tuotannon ja käytettävissä olevan pääomapanoksen
funktiona.
Työvoimantarvefunktio sisältää saman
informaation kuin tuotantofunktio, ratkaistu eri muuttujan suhteen.
- työvoimantarvefunktion ominaisuudet, missä
määrin malliin sisältyvä empiirinen versio on odotustemme
mukainen.
- tarkastelemme työvoimamarkkinoiden tarjontapuolta
eli työvoiman tarjonnan riippuvuuksia
- työttömyyden merkitys työvoimamarkkinoiden
tasapainon kannalta ja talouspolitiikan tavoitemuuttujana.
K43.1 Työpanoksen
kysyntä Suomen kansantaloudessa
|
(kuvio ja aikasarja on otettu TFEGRAF ohjelman
avulla AJKA61.TRE tietokannasta leikepöydälle ja kuvio tallennettu
edelleen PSP kuvankäsittelyohjelmalla GIF muotoon.)
|
| Kuviosta nähdään työllisyyden kehitys vuosina 1961-96.
Kuvioon on lisäksi piirretty vuosien 72-96 ja 87-96 eksponenttitrendit.
Vuosille 1997 ja 1998 on merkitty isolla pisteellä myös trendiennusteet.
Kuviossa näkyy selvästi työllisyyden poikkeama trendinsä
alapuolelle 70-luvun puolivälin jälkeisessä lamassa sekä
jyrkkä pudotus vuodesta 1990 lähtien. Viimeisten 10 vuoden trendissä
on yli 2.5 prosentin vuotuinen pudotus. Lyhyen tähtäyksen trendin
mukaan tehty trendiennuste näyttää kuitenkin menevän
vikaan, sillä havaintoaineiston loppupäässä on kaartumista
nousuun. - Tulostus on laadittu TreGraf
tietokoneohjelmalla. |
43.1
Tuotantofunktiosta työvoimantarvefunktioon
Siirtyminen tuotantofunktiosta työvoimantarvefunktioon
tapahtuu muutamalla yksinkertaisella matemaattisella operaatiolla. Lähtökohtana
on siis tuotantofunktio:
Kerrotaan yhtälön molemmat puolet tekijällä
L-b
Kerrotaan yhtälön molemmat puolet tekijällä
Q-1
Korotetaan
yhtälön molemmat puolet potenssiin -1/b
Otamme käyttöön uudet parametrit eli
eli
ja saamme tavoittelemamme työvoimantarvefunktion
43.1.1 Alenevan rajatuotoksen
laki
Miten tästä nähdään vallitseeko
vai ei alenevan
rajatuotoksen laki työpanoksen ja pääomapanoksen
suhteen? |
Työpanoksen
rajatuotos on tuotantofunktion osittaisderivaatta työpanoksen suhteen
Työpanoksen rajatuotos alenee, jos sen derivaatta
on negatiivinen. Siis derivoidaan vielä saatu rajatuotos uudelleen
eli otetaan toinen osittaisderivaatta
Lauseke on negatiivinen vain, jos b < 1,
sillä muuttujat voivat saada vain positiivisia arvoja.
Samalla tavoin saadaan ehdoksi pääoman rajatuotoksen
alenemiselle, että c < 1.
Äskeisten parametrien vastaavuuksien perusteella
työpanoksen rajatuotos on aleneva jos
Vastaavasti pääomapanoksen rajatuotos on aleneva
jos
Suomen kansantaloudesta selvitetty empiirinen työvoimantarvefunktio
- parametrien d ja e perusteella nähdään,
onko Suomen bruttokansantuotos saatu aikaan alenevan rajatuotoksen lain
vallitessa
- voimme päätellä, onko käyttäydytty
rationaalisesti ja otettu tuotannontekijöitä käyttöön
paremmuusjärjestyksessä
43.1.2 Suurtuotannon edut
Entä toinen tärkeä tuotantofunktion
ominaisuus,
suurtuotannon edut? Millä ehdoilla ne vallitsevat?
|
Taaskin tarkastelemme ensin alkuperäistä tuotantofunktiota.
Suurtuotannon edut
vallitsevat, jos kaikkien tuotantopanosten lisääminen
p prosentilla kasvattaa tuotantoa enemmän kuin p prosentilla.
Oletetaan aluksi panokset L = Lo
ja K = Ko. Niiden avulla tuotannon määrä
Nyt tuotannontekijäpanosten määrä
kerrotaan samalla luvulla q (= 1 + p/100), uudet panokset
ovat
Niillä uusi tuotannon määrä
Nähdään: jos
b+c > 1, silloin qb+c
> q ja Q1
> Q0
Jos taas
b+c < 1, silloin qb+c
< q ja Q1
< Q0
Suurtuotannon etujen olemassaolo riippuu siis alkuperäisen
tuotantofunktion parametrien summasta.
Vastaavasti työvoimantarvefunktion parametrein ilmaistuna
suurtuotannon edut vallitsevat, jos
EMPT = 1092.0 QGFF.63 KFAF-.40 R2 = .854
t 78 4.7 3.5 DW = 0.40
mrd 1985 mk 1989
EMPT työllistetty työvoima (1000) 2470
QGFF tuotantokustannushintainen bruttokansantuotos 345.6
KFAF tuotannollinen pääomakanta 1281.2
Tässä vuosien 63-89 havainnoista estimoidussa
työvoimantarvefunktiosta parametrien numeroarvot ovat: d
= .63 ja e = -.40.
Tulos on selvässä ristiriidassa sunnuntain Hesarin
kanssa.
- Tämän mukaan uusi työntekijä olisi
muka aina parempi kuin entinen, eli työpanoksen rajatuotos on nouseva.
Tämä lopputulos ei kuitenkaan missään
nimessä tee tyhjäksi sitä, että yritystasolla lisätyöntekijä
otetaan tuottavuusjärjestykseen asetettujen hakijoiden jonon tuottavammasta
päästä. Näin varmasti tehdään ja jäljelle
jää ainoastaan kaksi mahdollista selitystä:
- Havaintoaineistossa on vikaa. Eräs syy voisi olla,
että tässä käytetään pääomapanoksen
käytön asemesta pääomakantaa sellaisenaan. Kapasiteetin
käyttöastetta koskevia tietoja ei ole sellaisinaan käytettävissä,
mutta sellainen voitaisiin konstruoida käyttämällä
pääomapanoksen ja työpanoksen havaintojen suhdetta niiden
paikallisiin huippuarvoihin.
- Kysymyksessä on ns yhdistelyharha eli kokonaistason
havainnoista on hävinnyt päätöksentekotason ominaisuus,
kun havaintoja on laskettu yhteen. Näin voi tapahtua, kun kokonaiskäsitteet
sisältävät päätöksentekotason nousut ja laskut
'nettona'. Samanaikaisesti kun jokin yritys työllistää lisää
ja joutuu ottamaan heikkotuottoisempaa työvoimaa ja pääomakantaa,
jokin toinen yritys supistaa tuotantoaan ja sanoo irti työvoimaansa
ja poistaa pääomakantaa heikkotuottoisemmasta päästä.
- Vaikka molemmissa yrityksissä päätöksenteko
tapahtui juuri alenevan rajatuotoksen lain mukaisesti, kokonaisluvuissa
ei välttämättä näy mitään muutosta koska
supistumiset ja lisäykset kompensoivat toisensa.
Parametriarvojen mukaan on selvää, että
suurtuotannon edut vallitsevat, sillä
43.2 Työpanoksen
ja pääomapanoksen suhde
Malliin sisältyy aina kvantifioitua tietoa mallin
virheestä.
Malleihin sisältyy muutakin 'epätäsmällisyyttä'
tai vaihtoehtoisia mahdollisuuksia.
- työvoimantarvefunktio sisältää tiedon
työpanoksen ja pääomapanoksen keskinäisestä korvattavuudesta
- tuotanto voidaan aikaansaada käyttämällä
joko vähän työtä ja paljon pääomaa tai päinvastoin
rajakorvaussuhde,
joka ilmaisee kuinka monta yksikköä työpanos
vähenee, kun pääomapanosta lisätään yhdellä
yksiköllä.
Ja varmaan saadaan selville murjaisemalla
funktiosta derivaatta, vai kuinka? |
Aivan oikein. Työvoimantarvefunktion (osittais)derivaatta
pääomapanoksen suhteen ilmaisee montako henkilöä on
työllistettävä, jotta voitaisiin korvata pääomapanoksen
yhden miljardin markan supistuminen.
- kansantalouden työvoimantarvefunktiossa kysymys
on siitä, että pääomapanos (pääomakanta)
kasvaa jatkuvasti ja joudutaan toteamaan montako työntekijää
voidaan vähentää (tai joudutaan vähentämään)
kutakin yhden miljardin markan pääomapanoksen lisäystä
kohti.
Tarvitaan siis työvoimantarvefunktion osittaisderivaatta
pääomapanoksen suhteen. Tämä rajakorvaussuhde
on
Näin siis
- pääomapanoksen kasvu 1 mrd mk aiheuttaa 780
henkilön vähentymisen työllisyydessä eli
- yhden henkilön vapauttaa tuotannon palveluksesta
vähän yli miljoonan markan investointi eli
- pääomapanoksen lisäys jos tuotannon määrä
pidetään muuttumattomana.
Toisaalta:
- jos kysynnän kasvu edellyttää lisää
tuotantokapasiteettia, yhden miljoonan markan investoinnilla pystytään
luomaan yksi työpaikka
43.3 Työvoimantarvefunktion
joustot
Koska kysymyksessä on potenssimuotoinen funktio,
saadaan joustot suoraan parametrien arvoina. Kysymys on niiden tulkinnasta.
Joustot ovat
Työvoiman tarpeen jousto tuotannon määrän
suhteen ilmaisee yleisen jouston tulkinnan mukaan siis:
- Yhden prosentin tuotannon lisäys aiheuttaa .63 prosentin
lisäyksen työvoiman tarpeessa. Tuotannon kasvattaminen siis tietenkin
kasvattaa työvoiman tarvetta.
- Yhden prosentin suuruinen lisäys pääomapanoksen
suuruudessa aiheuttaa .40 prosentin supistumisen työvoiman tarpeessa.
Pääomapanoksen kasvattaminen siis supistaa työvoiman tarvetta.
Mutta eikö tässäkin voitaisi ajatella
lyhyen ja
pitkän tähtäyksen erottamista toisistaan? |
Kyllä vain. Tästä funktiosta niitä
ei tietenkään saada, mutta liittämällä mukaan
viivästetty selitettävä muuttuja selittäjäksi,
saadaan Koyckin muunnoksen kautta työvoiman tarpeen riippuvuus aikaisemmista
tuotannon määristä ja aikaisemmista pääomapanoksista.
Niitä voidaan pitää perusteltuina, koska työsuhteet
ovat pitkäaikaisia ja kerran hankittua pääomahyödykettä
käytetään kauan.
EMPT = 15.1 QGFF.40 KFAF-.28 EMPT1.61 R2 = .940
t 3.7 4.2 3.7 5.9 DW = 1.13
- selitysaste on tässä dynaamisen komponentin
sisältävässä yhtälössä tuntuvasti korkeampi
kuin edellä käsitellyssä staattisessa versiossa.
- t arvot ovat korkeat ja viivästetyn muuttujan mukaanotto
näyttää lohkaisevan huomattavan suuren osan vakiotermistä
selitettäväkseen.
Luonteva tulkinta olisi, että työvoiman kysyntää
on olemassa kolmesta syystä:
- (1) siksi, että työvoimaa tarvittiin edellisenäkin
vuonna ja
- (2) siksi, että halutaan saada aikaan tietty tuotannon
määrä sekä
- (3) siksi, että on olemassa tietty pääomakanta.
Lyhyen ja pitkän tähtäyksen joustojen selvittäminen
käy täsmälleen samalla tavalla kuin kulutusfunktioita tarkasteltaessakin.
43.3.1 Lyhyt tähtäys
Liitämme viivästetyn termin muitta mutkitta
vakioon, koska se ei edusta lyhyen tähtäyksen vaikutusta. Saamme
jokaiselle vuodelle eri vakion kuten lyhyen ja pitkän tähtäyksen
kulutusfunktiota muodostaessammekin. Vuoden 1989 havainnoilla operoiden
saamme:
Tästä lyhyen tähtäyksen (osittais)joustot
ovat: ELQs = .40 ja ELKs
= -.28
43.3.2 Pitkä
tähtäys
Luvun alussa olevasta kuviosta K43.1 nähdään,
että pitkällä tähtäyksellä työvoiman
tarve kasvaa 0.8 prosenttia vuodessa, eli ensi vuoden työvoimantarve
on 1.008 kertaa tämän vuoden työvoiman tarve tai viime vuoden
työvoiman tarve oli 99.2 prosenttia tämänvuotisesta.
Pitkän tähtäyksen työvoimantarvefunktioksi
saamme:
EMPT1-.61 = 15.1 * QGFF.40
KFAF-.28
EMPT = 15.12.56 * QGFF.40*2.56
KFAF-.28*2.56
EMPTl = 1043 * QGFF1.02
KFAF-.72
Tästä pitkän tähtäyksen (osittais)joustot
ovat:
ELQl = 1.02 ja ELKl
= -.72
Tämän mukaan siis hyvin huomattava osa tuotannon
ja pääomapanoksen työllisyysvaikutuksista toteutuu vasta
seuraavina vuosina.
43.3.3 Laskelmia
joustoilla
Luonteva kysymys:
Paljonko kysynnän olisi kasvettava, jotta työllisyys
ei supistuisi?
Paljonko kysynnän olisi kasvettava, jotta vapautuva
työpanos sidottaisiin edelleen tuotantoon?
Vastaus työvoimantarvefunktion
avulla.
- Ensiksi on selvitettävä, kuinka suurta nettopääomanmudostus
on eli mikä on olemassa olevan pääomakannan vuotuinen kasvu.
- Voimme tarkastella asiaa yleisemmin ja selvittää
pitkän tähtäyksen trendistä kasvuprosentin tai tarkastella
yksittäisiä vuosia, esim. viimeisen saatavissa olevan vuoden
tiedon.
- Nämä tiedot saamme TREGRAF ohjelmalla tai kuviosta
K43.2.
K43.2
Pääomakanta Suomen kansantaloudessa
|
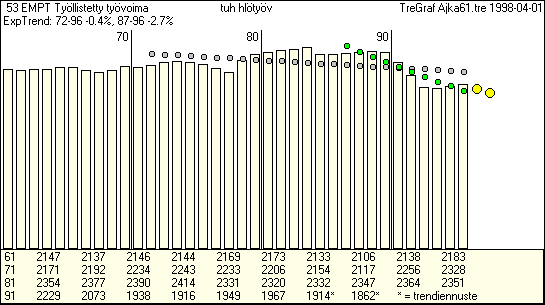
(kuvio ja aikasarja on otettu TFEGRAF ohjelman
avulla AJKA61.TRE tietokannasta leikepöydälle ja kuvio tallennettu
edelleen PSP kuvankäsittelyohjelmalla GIF muotoon.)
|
| Kuviosta nähdään pääomakannan kehitys vuosina
1961-96. Kuvioon on lisäksi piirretty vuosien 72-96 ja 87-96 eksponenttitrendit.
Viimeisten 10 vuoden trendikasvu on 1.8 prosenttia. Tätä käyttäen
on vuosille 1997 ja 1998 merkitty isoilla pisteillä myös trendiennusteet.
- Tulostus on laadittu TreGraf
tietokoneohjelmalla. |
Kuviossa K43.2 esitetyn trendikasvutiedon mukaan pääomakanta
on siis kasvanut vuosina 71-95 keskimäärin 3.0 prosettia vuodessa.
- työpanosta on normaalisti vapautunut noin 1.2 (=.40
x 3.0) prosenttia (= 25 000 henkilöä).
- yhden prosentin tuotannon kasvu vaatii .63 prosentin
työpanoksen kasvun,
- tuotannon kasvun on oltava noin 2 (=1.2/.63)prosenttia,
jotta se työllistäisi uudelleen pääomapanoksen kasvun
vapauttaman työvoiman
- tämä ei vielä riitä pitämään
työttömyyttä kurissa, sillä työvoiman tarjonta
työntää myös lisää työllistettäviä
työvoimamarkkinoille.
43.4 Työvoiman tarjonta
Kuinka suuri työvoiman tarjonnan kasvu sitten
on
ja mistä tekijöistä se riippuu? |
Työvoimamarkkinoiden perusyhtälö on
eli työttömyys U on työvoiman tarjonnan
EK ja työvoiman kysynnän EM erotus.
- vastaa työvoimamarkkinoiden osalta hyödykemarkkinoiden
tasapainoehtoa
- työvoimamarkkinoiden perusyhtälö ei ole
tasapainoehto
- työvoimamarkkinat eivät ole tasapainossa, vaan
työttömyyden verran epätasapainossa.
K43.3
Työttömyys Suomen kansantaloudessa
|
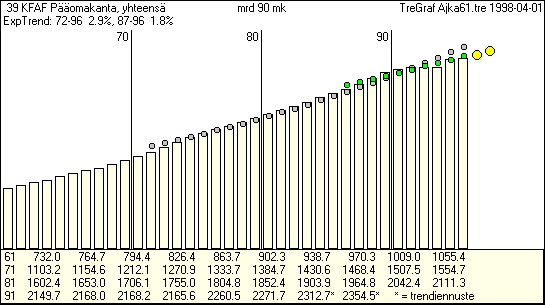
(kuvio ja aikasarja on otettu TFEGRAF ohjelman
avulla AJKA61.TRE tietokannasta leikepöydälle ja kuvio tallennettu
edelleen PSP kuvankäsittelyohjelmalla GIF muotoon.)
|
| Kuviosta nähdään työttömyyden kehitys vuosina
1961-96. Kuvioon on lisäksi piirretty vuosien 72-96 ja 87-96 eksponenttitrendit
sekä merkitty isoilla pisteillä myös trendiennusteet.
Mutta tässä tapauksessa trendi on erittäin heikko
ennusteväline. Tarvitaan talousteoriaa, eikä sittenkään
voida odottaa tarkkaa ennustetta. - Tulostus on laadittu TreGraf
tietokoneohjelmalla. |
Tietenkin työvoiman tarjonnan kuten kaikkien muidenkin
'kaikki riippuu kaikesta' tyyppisen selitysmallin muuttujien takana on
monia tekijöitä.
- Klassisen, siis ennen Keynesiä vallinneen talousteorian
mukaan nimellispalkka tasapainottaa täydellisesti työvoimamarkkinat
samalla tavoin kuin hinta tasapainottaa hyödykkeen kysynnän ja
tarjonnan.
- Epätasapainotekijäksi voi korkeintaan jäädä
ns. luonnollinen työttömyys eli työttömyys, joka johtuu
työpaikan vaihtamisesta yms tekijöistä.
- Mutta Keynesin mukaan palkka ei toimi kuten hinta. Se
on alaspäin jäykkä, eli ei painu alaspäin ylitarjonnan
poistamiseksi.
Toinen komplikaatio, joka saattaa saada työvoimamarkkinoiden
epätasapainon ulottumaan ohi luonnollisen työttömyyden on,
että
- työnantajapuoli (työvoiman kysyntä) kiinnittää
työpanoksen rajatuotos mielessään huomiota vain reaalipalkkaan,
kun taas
- työntekijäpuoli (työvoiman tarjonta) pitää
silmämääränään kompensaatiota inflaation
syömästä ostovoimasta ja siis reagoi vain nimellispalkkaan.
AJKA mallissa työvoiman tarjonta on riippuvainen
vain viivästetystä työvoiman tarjonnasta ja työikäisen
väestön määrästä, siis demograafisesta tekijästä.
Kun riippuvuuksia palkkatasosta on kokeiltu, niistä ei yllättävää
kyllä, ole saatu tilastollisesti merkitseviä parametriarvoja.
Tämän tekstin laatimishetkellä käytössä oleva
yhtälö on
EMPK = - 183 + .85 EMPK1 + .18 AGEW R2 = .971
t 1.2 8.6 1.6 DW = 1.54
AGEW Työikäinen väestö (ikäluokat 15-64) tuhatta 17341
ExpTrend: 71-95 0.4%, 86-95 0.3%
61 2824 2872 2916 2945 2971 2997 3031 3053 3049 3052
71 3081 3109 3136 3157 3175 3185 3194 3208 3221 3241
81 3259 3282 3307 3330 3342 3345 3346 3343 3350 3360
91 3362 3383 3401 3421 3412
EMPK Työvoima tuh hlötyöv R960920
ExpTrend: 71-95 0.3%, 86-95 -0.5%
61 2171 2162 2176 2174 2197 2205 2192 2187 2196 2224
71 2220 2247 2285 2282 2284 2297 2291 2286 2399 2442
81 2481 2526 2534 2549 2460 2458 2462 2463 2453 2439
91 2422 2401 2382 2372 2366
Normaali työvoiman tarjonnan kasvu on vuosien 65-89
eksponenttitrendin mukaan 0.8 prosenttia eli noin 20 000 henkeä vuodessa.
- Tämä merkitsee lisätyöllistettäviä,
niin että kokonaiskysynnän kasvun on sidottava vielä nämäkin.
Tarvittava tuotannon lisäkasvu on noin 1.2 (=0.8/.63) prosenttia.
- Tämä on lisättävä pääomapanoksen
kasvun vapauttaman työpanoksen vaatimaan tuotannon kasvuun, joka keskiarvoluvuilla
laskien oli noin 3 prosenttia.
- Näin siis tuotannon kasvun olisi ollut oltava vähän
yli 4 prosenttia, jotta työttömyys ei olisi kasvanut.
Tustuttuasi nyt muutamiin työvoimantarvefunktiota
koskeviin näkökohtiin voit kokeilla AJK ohjelmaa, joka laskee
erilaisilla olettamuksilla kysynnän kasvua, joka tarvitaan pitämään
työttömyyden kasvu kurissa. Tätä varten on käytettävissäsi
EMPLOY
demo-ohjelma.
Lähteitä
C W Cobb and P H Douglas: 'A Theory of Production', AER
Vol 18, No 1 (March 1928), pp. 139
L R Klein and R S Preston: 'The Measurement of Capacity
Utilization, American Economic Review Papers and Proceedings Vol 53, No
2 (May 1963) pp. 275-92.
AJK kotisivu o PerMak
ohjelmasivu o Kansantalouden kurssit
o Makrotaloustieteen perusteet
Asko Korpela 980503 (970316) o Asko.Korpela@kolumbus.fi
(palaute)
[ccc]