23 Perusteoria ja Suomen kansantalous [ccc]

o Kulutuksen suuruus ja rakenne
K23.1 Yksityinen kulutus ja tulot Suomessa
K23.2 Yksityinen kulutus Suomen kansantaloudessa
23.1 Keynesiläinen kulutusfunktio
1.1 Talousteoreettiset näkökohdat
o Rajakulutusalttius
o Kulutuksen jousto
23.2 Kulutus ja tulovirran pituus
2.1 Suhteellisen tulon hypoteesi
2.2 Pysyväistulohypoteesi
o Olettamukset
o Pysyväistulohypoteesi ja Suomen kansantalous
o Lyhyt ja pitkä tähtäys
o Kulutuksen tulojoustot
2.3 Elinkaarihypoteesi
o Tuleva tulo
o Kulutus on suunnitelma
23.3 Muut kulutukseen vaikuttavat tekijät
o Erot tuloriippuvuudessa.
o Asennetekijät.
o Entä inflaatio

Vapaaehtoinen harjoitustehtävä: PerMakH23

Tietokoneohjelmat: Tregraf o Kulutuksen rakenne o Koyck-ohjelma o WregAjk

'Pikahaku': o Lyhyt ja pitkä tähtäys o Joustot o Yksityinen kulutus on suurin o Kulutustiedot o Parkin

Kyselijä:
Voiko siis kansantalouden tilinpidossa ...
Mikä ero on trendiennusteella ja trendiarvolla?
Eipä mennä asioiden edelle.
Miten voidaan selvittää tuleva tulo
Entä inflaatio?
Hetkinen!

Liite: Koyckin muunnos

Makrotaloustieteen perusteet o Kansantalouden kurssit o AJK kotisivu

Parkin:
[Saving and Consumption Decisions 601 Real Interest Rate 601 Disposable Income 601 Purchasing Power of Net Assets 601 Expected Future Income 602 Consumption Demand and Saying Supply 602 Disposable Income, Consumption Expenditure and Saving 604 Other Influences on Consumption Expenditure and Saving 605 Consumption Demand and Saving Supply in the United States 606 ]

Yksityinen kulutus on kokonaiskysynnän suurin komponentti. Jos haluat perehtyä yksityisen kulutuksen rakenteeseen, saat yleiskuvan kokeilemalla tietokoneohjelmaa KULURAK. Se näyttää yksityisen kulutuksen jakautumisen pääkompponentteihinsa ja niissä tapahtuneen kehityksen.

Tutustu

yksityisen kulutuksen komponentteihin, niiden osuuksiin kokonaiskulutuksesta ja pitkän ja lyhyen tähtäyksen trendeihin. Miten 90-luvun lama näkyy niissä?

K23.1 Yksityinen kulutus ja tulot Suomessa

Tässä kurssissa ei niinkään kiinnitetä huomiota kulutuksen rakenteeseen kuin sen suuruuteen ja kokonaistaloudellisiin syihin ja seurauksiin. Kulutuksen suuruus riippuu käytettävissä olevasta tulosta, aikaisemmasta, nykyisestä ja tulevasta tulosta.

Yksityinen kulutus on yli puolet bruttokansantuotoksesta, joten sen riippuvuuksien ymmärtäminen, muutosten ennustaminen on luontevasti makroanalyysin enimmäinen tehtävä. Tehtävä on mielenkiintoinen ja palkitseva, sillä järkeenkäyvää ja vivahteikasta teoriaa on runsaasti ja varsin hyvään selityskykyyn ja ennustettavuuteen päästään helposti.

Seuraavassa tarkastellaan kulutuksen riippuvuutta käytettävissä olevasta tulosta, nettovarallisuuden ostovoimasta ja odotettavissa olevasta tulokehityksestä. Itse asiassa nämä kaikki ovat lopulta käytettävissä olevan tulon eri aspekteja.

Voi. Kysymys on siitä, kuinka pitkälle ajanjaksolle jakautunut tulovirta vaikuttaa kulutukseen. Myös eri tulotyypeillä on jossain määrin erilaiset vaikutukset kulutukseen. Samoin kulutuksen tyypillä on merkitystä, sillä esim päivittäisten kulutushyödykkeiden hankinnan riippuvuudet ovat erilaiset kuin kestokulutushyödykkeiden hankinnan riippuvuudet.

K23.2 Yksityinen kulutus Suomen kansantaloudessa, mrd 90 mk

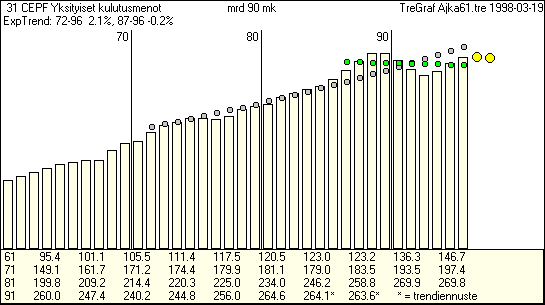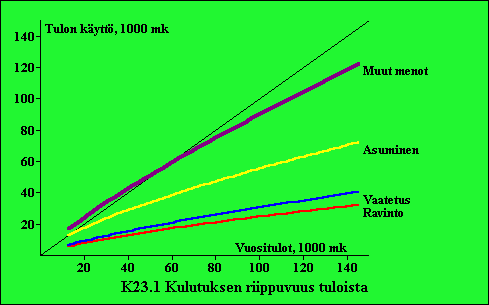
Kuviosta nähdään yksityisen kulutuksen kehitys vuosina 1961-96. Kuvioon on lisäksi piirretty trendiennusteet vuosille 97 ja 98 sekä vuosien 72-96 ja 87-96 eksponenttitrendit. Kuvio on laadittu TreGraf tietokoneohjelmalla, jolla voit nähdä myös prosenttimuutokset ja tarkastella trendien avulla kehitystä haluaminasi aikajaksoina.

Siitähän oli jo puhe luvun 2 lopussa. Kertaa vielä se kohta ennenkuin jatkat, sillä trendi on hyvin hyvä keino saada ote aikasarjan ytimestä. Sitäpaitsi trendi on eräänlainen nollavaihtoehto mille hyvänsä teorialle. Vähimmäisvaatimus talousteorialle on, että sen pitää pystyä selittämään menneisyys paremmin kuin sen tekee trendi.

TreGraf Aikasarjatietokannan grafiikka ja trendit

Tutustu

keskeisiin yksityisen kulutuksen muuttujiin, niiden minimi- ja maksimimuutoksiin, trendeihin ja standardi-poikkeamiin.

23.1 Keynesiläinen kulutusfunktio

Yksinkertaisin hypoteesi

Tämä tuntuu niin luonnolliselta ja luontevalta ajatukselta, että tarvitaan hyvin utelias ja ennakkoluuloton ihmettelijä ehdottamaan jotakin muuta. Mutta näitä ihmettelijöitä on ollut. Ja heidän ajatuksensa voidaan esittää somalla tavalla loogisesti laajenevana sarjana.

Kaikki alkoi oikeastaan siitä, kun J.M. Keynes esitti kulutuksen ja tulojen välisen riippuvuuden keskeisenä makrokäsitteenä kansantulo-mallissaan:

Y = C + I + G
C = a + b Y      a > 0, 0 < b < 1

Keynes puhui 'perustavaa laatua olevasta psykologisesta laista', jonka mukaan

• kulutus kasvaa tulojen kasvaessa, mutta tulojen kasvaessa
• kulutukseen käytetään pienenevä osuus tuloista.

Jos Suomen kansantaloudesta estimoidaan tämän mukaan
vuosien 1968-95 tiedoista kulutusfunktio, saadaan

CEPF = - 0.3 + .97 YDPF R2 = .992 
 t       0.1    58      DW = 0.55 

mrd 1990 mk                                           1990 
YDPF yksityinen käytettävissä oleva tulo               270 
CNSF kertakulutushyödykkeiden ja palvelusten kulutus   268 

{ KULUTUS.REG   (62-90)   5 CEPF CNST YDPF }  97-02-22  19:54
CEPF   = { Yksityiset kulutusmenot                                    mrd 90 mk    }
-    0.3 {* CNST  0.1  Sarja ykkösiä vakiotermin laskemiseksi                      }
+ 0.9703 * YDPF {   64 Yksityinen käytettävissä oleva tulo            mrd 90 mk    }
{ F   3408 (1,25)    t,  R² 0.9924,  DW  0.55,  SD    4.1,  Ro  0.79 (1998-01-25) } ;

1.1 Talousteoreettiset näkökohdat

Nähdään, että Keynesin perushypoteesi kulutusosuuden pienenemisestä tulojen kasvaessa ei pidä kansantalouden kulutusfunktiossa paikkaansa. Kulutuksen prosenttiosuuden pieneneminen näkyy, jos lasketaan tämän mallin mukaan kulutuksen arvot vuosina 1963 ja 1989.

1963: - 0.3 + .97(107.1) = 103.5 = 96.7% tuloista 
1989: - 0.3 + .97(268.2) = 259.8 = 97.0% tuloista 

Kulutuksen prosenttiosuuden kasvaminen näkyy jo valitusta funktiomuodosta.

• Tässä käytetty lineaarinen funktiomuoto takaa, että kulutuksen suhteellinen osuus kasvaa tulojen kasvaessa, koska kulutus on sen mukaan 97 prosenttia tuloista miinus 0.3 mrd mk.
• Kun kiinteä summa vähennetään suuremmasta luvusta (kulutuksesta 1989), se pienenee suhteellisesti vähemmän kuin jos se vähennetään pienemmästä luvusta (kulutuksesta 1963).
• Siis Keynesin väittämä merkitsee lineaarista kulutusfunktiota käytettäessä, että vakiotermin tulee olla positiivinen.
• Tässä havainto-aineistossa se sitä juuri ja juuri ei ole.

Rajakulutusalttius eli kulutusfunktion derivaatta tulojen suhteen on
lineaarisen kulutusfunktion tapauksessa MPC = .97.

Rajakulutusalttius

Johtopäätös:

• Rajakulutusalttius ilmaisee siis tässä, että käytettävissä olevan
• tulon lisäys 1 mrd mk aiheuttaa kulutuksen lisäyksen 970 milj mk. Tai,
• koska malli on lineaarinen, tulkinta voi olla myös:
• markan lisäys tuloissa johtaa 97 pennin lisäykseen kulutuksessa.

Kulutuksen jousto

Edelleen tätä kulutusfunktiota analysoitaessa muistetaan, että yleisesti funktion y = f(x) ja erityisesti lineaarisen funktion y = a + b x joustot ovat:

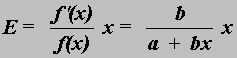
eli lineaarisessa kulutusfunktiossa C = a + b Y jousto riippuu tulotasosta Y. Sen mukaan saadaan tässä käytetystä lineaarisesta kulutusfunktiosta kulutuksen tulojoustoksi esim vuodelle 1989 (tiedot 1985 mrd mk; vanha laskelma)

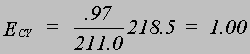
Tämän mallin mukaan siis:

Johtopäätös:

Jousto ilmaisee, että tulojen kasvu yhdellä prosentilla johtaa kulutuksen kasvuun 1.0 prosentilla.

Tehtävä:

Laske vastaava kulutuksen tulojousto vuodelle 1963, kun vuoden 1963 tulot ovat 85.6 mrd mk ja kulutuksen laskettu arvo 82.1 mrd mk

23.2 Kulutus ja tulovirran pituus

Edellä luvattu tulokäsitteiden laajeneva sarja sisältyy kolmeen väittämään eli hypoteesiin:
1 Suhteellisen tulon hypoteesi
2 Pysyväistulohypoteesi
3 Elinkaarihypoteesi

Näistä ensimmäisessä tarkasteluun otetaan kuluvan kauden tulon lisäksi edellinen tulohuippu. Pysyväistulohypoteesissa otetaan huomioon nykyisen lisäksi koko menneisyyden tulojakauma ja elinvaihehypoteesissa paitsi menneisyys ja nykyisyys, myös tulevaisuus, koko elinaikainen tulo.

2.1 Suhteellisen tulon hypoteesi

Vaatimattomin askel kohti laajempia tulokäsitteitä on suhteellisen tulon hypoteesi, jonka Duesenberry esitti 1949. Sen mukaan

• Kuluttaja ei niinkään välitä kulutuksen absoluuttisesta tasosta kuin kulutuksensa tasosta suhteessa muiden kuluttajien kulutukseen.
• Kulutus ei riipu ainoastaan tämän hetken tuloista, vaan aikaisemmin saavutetusta kulutuksen tasosta.

Edellisen mukaan kuluttaja kokee siis hyötyfunktionsa arvon nousua vain jos hänen kulutuksensa kasvaa keskimääräiseen kulutukseen verrattuna. Tämän mukaan kuluttaja, jonka tulot ovat keskitason alapuolella, joutuu käyttämään keskimääräistä suuremman osuuden tuloistaan ylläpitääkseen 'yhteiskunnallisen standardin' mukaista kulutusta. Vastaavasti keskituloa suuremmilla tuloilla elävä tarvitsee pienemmän osuuden tuloistaan kulutukseen. Jos tulot kasvavat ja tulonjako pysyy muuttumattomana, myös kulutuksen osuus tuloista c/y pysyy vakiona.

Alunperin Duesenberry esitti jälkimmäisen hypoteesinsa keskimääräistä säästämisalttiutta s/y koskevana, mutta koska kulutusalttius on c/y = 1 - s/y, saadaan suhteellisen tulon hypoteesin mukaiseksi makrotason kulutusfunktioksi

C/Y = a + b Y/Y₀    b < 0

Käytännössä edellinen tulohuippu Y₀ on edellisen vuoden tulo. Kuitenkin Suomen kansantaloudessa vuoden 1976 käytettävissä oleva tulo oli pienempi kuin vuoden 1975 tulo ja vielä vuoden 1977 tulokin oli pienempi kuin vuoden 1976 tulo. Käytettävissä oleva tulo pienentyi siis kahtena vuonna peräkkäin ja vuonna 1978 edellinen tulohuippu oli vuoden 1975 käytettävissä oleva tulo.

2.2 Pysyväistulohypoteesi

Selvä laajennus Duesenberryn tulokäsitteeseen verrattuna on Friedmanin pysyväistulohypoteesin mukainen tulo. Siinä otetaan huomioon, ei ainoastaan edellinen tulohuippu, vaan lopulta kuluttajan koko aikaisempi tulojakautuma. Pysyväistulohypoteesin mukaan kuluttajan päätöksenteko tapahtuu pääasiassa tulojen pysyväiskomponentin mukaan.

Olettamukset

Tulossa Y ja kulutuksessa C voidaan erottaa pysyvä p (=permanent) ja tilapäinen t (=transitory) komponentti.

Y = Y_p + Y_t
C = C_p + C_t

Näiden väliset yhteydet voidaan esittää muodollisesti seuraavien lauseiden avulla. Pysyvä ja tilapäinen komponentti eivät riipu toisistaan eli niiden välinen korrelaatio r on nolla. Myös tilapäisen kulutuskomponentin ja tilapäisen tulokomponentin välinen korrelaatio oletetaan nollaksi eli nekään eivät riipu toisistaan.

r(Y_p,Y_t) = 0    r(C_p,C_t) = 0    r(Y_t,C_t) = 0

Tilapäiskomponenttien odotusarvo (keskiarvo) on nolla.

E(Y_t) = 0    E(C_t) = 0

Seuraavaksi pyritään osoittamaan, että tietyllä tavalla aikaulottuvuudessa muodostunut tulojakauma edustaa pysyväistuloa. Tämä tapahtuu ns Koyckin muunnoksen avulla.

Voidaan osoittaa, että muotoa

C = a + b C1 + c Y    (2.3.1)

C = kulutus
Y = käytettävissä oleva tulo
C1 = viivästetty kulutus

oleva kulutusfunktio

• Sisältää pitkälle aikavälille jakautuneen tulomuuttujan vaikutuksen.
• Koska tulomuuttujan vaikutus on pitkälle aikavälille jakautunut ja pysyväistulohypoteesin mukaan tilapäiskomponentin odotusarvo on nolla, tämä funktio on Friedmanin pysyväistulohypoteesin mukainen kulutusfunktio.

Pysyväistulohypoteesi ja Suomen kansantalous

Edellä AJKC mallin yhteydessä esitettiin jo Friedmanin pysyväis-tulohypoteesin mukainen kulutusfunktio, mutta se oli estimoitu juoksevahintaisista havainnoista. Oikeastaan teoriat koskevat kulutuksen määriä eikä arvoja, joita juoksevahintaiset havainnot kuvaavat. Seuraavassa on käytetty vuosien 1963-89 havaintoja vuoden 1985 hinnoin.

CEPF = - 0.2 + .49 YDPF + .52 CEPF1   RR = .995 
 t       0.1   3.2        3.2         DW = 0.86 
                                           1989 
YDPF yksityinen käytettävissä oleva tulo  218.5 
CEPF yksityinen kulutus                   218.2 
CEPF1 viivästetty (= vuoden 1988) CEPF    210.0 

Tästä voidaan tunnistaa

• Koyckin muunnoksen parametrit k = .49 ja q = .52. Niiden avulla
• voidaan laskea esim viiden vuoden takaisen tulon kertoimeksi k q⁵ = .49(.52)⁵ = .019. Vuoden 1984 tulo oli 184.5. Tästä voidaan siis laskea vuoden 1989 kulutuksen 218 mrd mk selitykseen tulevan siivun olevan .019(185) = 3.4 mrd mk eli vajaat kaksi prosenttia vuoden 1989 kulutuksesta.
• Vain noin puolet eli .49(218) = 107 mrd mk selittää saman vuoden eli vuoden 1989 tulo.
• Näin siis vuosien 1985-88 tulot eli tulojakauma selittää varsin suuren osan vuoden 1989 kulutuksesta.

Yksinkertaistettu johtopäätös:

• noin puolet kulutuksesta on sidottu saman kauden tuloihin ja
• puolet aikaisempiin kulutustottumuksiin.

Tätä pysyväistulohypoteesin mukaista tulojakautuman merkitystä kulutuksen selittäjänä voit kokeilla pienellä Koyck tietokoneohjelmalla.

• antaa ensin suuren painon aikaisemmille tuloille ja pienen saman vuoden tulolle ja sitten
• siirtää painoa kohti nykyhetkeä.
• niiden vuosien luku pienenee, jotka antavat yli prosentin lisän kulutuksen selitykseen.

Lyhyt ja pitkä tähtäys

Tulojakautuman vaikutuksen analyysi voidaan tiivistää kahdeksi luvuksi lyhyen tähtäyksen ja pitkän tähtäyksen rajakulutusalttiuksiksi. Lyhyen tähtäyksen rajakulutusalttiudessa kysymys on siitä, mikä osa tulojen muutoksen vaikutuksesta toteutuu samana vuonna kuin tulon muutos tapahtuu. Pitkän tähtäyksen rajakulutusalttiudessa taas ajatus on: paljonko tulon muutoksesta aiheutuu kulutuksen muutosta kaikkiaan eli pitkällä tähtäyksellä.

Lyhyen tähtäyksen rajakulutusalttius selviää saadusta funktiosta välittömästi, sillä vaikutuksiahan ei voi tulla lainkaan viivästetyn kulutuksen eli CEPF1 termin kautta. Siis koko termi .52 CEPF1 on rinnastettavissa vakioon. Sen mukaan saammekin lyhyen tähtäyksen kulutusfunktioksi:

CEPF = (- 0.2 + .52 CEPF1) + .49 YDPF

Tästä seuraa tietenkin kokonainen sarja lyhyen tähtäyksen kulutusfunktioita, jokaiselle tarkasteltavalle vuodelle omansa. Ne eroavat toisistaan vakion suhteen. Kulmakerroin niissä on kaikissa sama .49.

Lineaarisen kulutusfunktion kulmakerroin on myös samalla rajakulutusalttius eli kulutusfunktion derivaatta tulojen suhteen. Lyhyellä tähtäyksellä se on siis

MPC_s = dCNSF/dYPDF = .49

Johtopäätös:

Yhden (mrd) mk tulojen muutos aiheuttaa samana vuonna 0.49 (mrd) mk muutoksen yksityisessä kulutuksessa.

Pitkän tähtäyksen rajakulutusalttiuden selvittäminen on sekin vain piirun verran mutkikkaampi juttu. Ensiksikin toteamme REGAJK laskelmien tulostuksesta, että kulutus kasvaa vuosien 65-89 eksponenttitrendin mukaan 3.4 prosenttia (jos lamakausi otetaan mukaan, saadaan vastaava kasvu 2.1 % kuviosta K23.2) vuodessa. Tämän 25 vuoden havainnoista lasketun trendin voimme katsoa kuvaavan kulutuksen muutosta pitkällä tähtäyksellä. Sen mukaan siis aina seuraavan vuoden kulutus on 3.4 prosenttia suurempi kuin edellisen eli tässä noudatettua merkintätapaa käyttäen:

CEPF = 1.034 CEPF1 eli CEPF1 = CEPF / 1.034 tai CEPF1 = .97 CEPF

Nyt emme yhdistäkään viivästettyä termiä vakioon, vaan selitettävään muuttujaan. Se tapahtuu äskeistä kulutuksen ja viivästetyn kulutuksen välistä suhdetta käyttäen seuraavasti:

CEPF = - 0.2 + .52 (.97 CEPF) + .49 YDPF
CEPF (1 - .50) = - 0.2 + .49 YDPF
CEPF = - 0.2/.50 + .49/.50 YDPF
CEPF = - 0.4 + .98 YDPF

Loppu käy helposti. Meillä on pitkän tähtäyksen kulutusfunktio. Siitä saadaan rajakulutusalttius derivoimalla kuten tavallisesti:

MPC_l = dCNSF/dYPDF = .98

Johtopäätös:

Yhden (mrd) mk tulojen muutos aiheuttaa pitkällä tähtäyksellä eli saman ja seuraavien vuosien aikana kaikkiaan .98 (mrd) mk muutoksen yksityisessä kulutuksessa.

Joustot. Tietenkään emme unohda joustoja. Jousto on loppujen lopuksi kaikkein yleispätevin muutoksen mitta, koska siinä mittayksikkö on aina sama, prosentti: prosenttimuutoksen vaikutus mitattuna prosenteissa. Ja prosenttimuutoksen suuruudesta kaikilla ihmisillä on konkreettinen mielikuva. Pysyväistulohypoteesin mukaisesta kulutusfunktiosta saamme kulutuksen tulojoustot erikseen lyhyellä ja pitkällä tähtäyksellä, molemmat sijoittamalla asianomaiset tiedot jouston kaavaan. Tässä vuodelle 1989 joustot ovat

Johtopäätös:

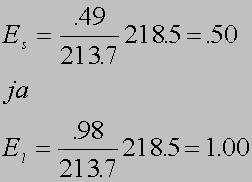
Yhden prosentin suuruinen tulojen muutos aiheuttaa lyhyellä tähtäyksellä eli vuoden sisällä noin puolen (.50) prosentin ja pitkällä tähtäyksellä eli saman ja seuraavien vuosien aikana kaikkiaan 1.00 prosentin suuruisen muutoksen yksityisessä kulutuksessa.

2.3 Elinkaarihypoteesi

Tuleva tulo o Kulutus on suunnitelma

Viimeisenä vaiheena tulokäsitteen laajentamisessa on elinvaihe- tai elinkaarihypoteesi. Sen ovat lähdetietojen mukaan ensimmäisenä esittäneet Ando ja Modigliani. Elinvaihehypoteesin mukaan kulutukseen ei vaikuta ainoastaan samanaikainen tai aikaisempi tulo, vaan myös tuleva tulo. Ensi näkemältä tämä saattaa tuntua varsin utopistiselta, mutta tarkemmin ajatellen asia onkin päivänselvä. Ainoa hankaluus on tulevan tulon mittaaminen. Miten se voisi tapahtua?

Ajatellaanpa kahta nuorukaista, jotka juuri ovat lopettaneet koulunsa ja astuvat elämään. Toinen ei ole lainkaan menestynyt koulussa ja joutuu sen vuoksi etsimään työtä mitä saa. Toinen taas on osoittanut huippukyvykkyyttä jo koulussa ja parhaat opintopaikat ovat hänelle avoimena. Hän on juuri päässytkin lääketieteelliseen tiedekuntaan. Kumpikin menee pankinjohtajan puheille. Lainaa pitäisi saada elämän aloittamiseen.

Miten pankinjohtaja suhtautuu? Luultavasti myönteisemmin lahjakkaan pojan toiveisiin kuin elämän kääntöpuolelle joutuneen toiveisiin. Emmekä voi siitä pankinjohtajaa moittia. Niin me itsekin tekisimme. Siis tulevaisuuden näkymät vaikuttavat kulutusmahdollisuuksiin. Vaikutus ei koske vain rahansaantia eli reaalisia kulutusmahdollisuuksia vaan myös asenteita. 'Lääkikseen' päässyt itsekin asennoituu elämäänsä kuin puolivalmis tohtori. Ja kulutus on sen mukaan.

Enpä tosiaan. Mutta kikat on tähänkin keksitty. Eikö vain meistä jokainen ole joskus jo mummon sylissä istuessaan haaveillut, että jos mummo olisi nuorena tyttönä hoksannut panna satasen tilille, niin nyt olisi niin ja niin paljon rahaa. Voitaisiin ostaa vaikka talo. Korkoa olisi kertynyt aivan hirveästi. Siis nykyinen pesämuna tuottaa korkoa pitkälle tulevaisuuteen. Asia voidaan ajatella myös nurinpäin: tällä hetkellä olemassa oleva talletus on ikäänkuin kaikkien tulevaisuuden tulojen diskontattu nykyarvo. Siispä liitetään kulutusfunktioonkin talletusten reaaliarvo markkeeraamaan tulevaa tuloa. Varmaan itse kukin meistä kuluttaisi eri tavoin jos pankissa olisi miljoonan markan talletus vaikka tulot olisivatkin täsmälleen samat kuin naapurilla, jolla miljoonaa ei ole.

Näiden sinänsä mikrotason perusteluiden jälkeen rohkenemmekin liittää makrotason kulutusfunktioon lisäselittäjäksi reaalitalletukset, jotka saadaan kun nimellistalletukset jaetaan kutuksen deflaattorilla eli kuluttajahinnoilla.

CEPF = 5.9 + .62 YDPF + .19 CEPF1 + .24 DETF  R2 = .998 
 t     3.7   6.5        1.8         6.5       DW = 2.03 

mrd 1985 mk                                        1989 
YDPF yksityinen käytettävissä oleva tulo          218.5 
CEPF yksityiset kulutusmenot                      218.2 
DETF reaalitalletukset                            165.5 

Ja hokkus pokkus, se onnistui.

• Selitysaste kohosi entisestään.
• Kaikki parametrit ovat tilastollisesti merkitseviä t-arvolla mitattuna.

• Tästä lyhyen tähtäyksen tulkinta on, että tulojen muutos (mrd) markalla kasvattaa kulutusta .62 (mrd) markalla. Ja talletusten kasvu (mrd) markalla lisää kulutusta .24 (mrd) markalla.
• Pitkän tähtäyksen vaikutukset saadaan jakamalla nämä parametrit luvulla (1-.19 = .81) kuten edellä näimme. Saadaa = .30.
• Tietenkin voimme laskea myös vastaavat joustot, jotka ovat eri suuret eri vuosille, kuten aina lineaarisen funktion joustot.

Elinvaihehypoteesin mukaan kulutuspäätös on kuin suunnitelma,

jossa aina lähdetään olemassa olevien voimavarojen pohjalta, mutta tähdätään kuitenkin tulevaisuuteen. Sunnitelma voi kattaa pitkänkin aikajakson. Sitä tarkistetaan jatkuvasti uusien näkymien ja olemassa olevien resurssien mukaan.

Tästä saat käyttöösi c:\ajk\kok kansioon WREGAJK.EXE tietokoneohjelman

Tutustu

keskeisiin kulutusta koskeviin hypoteeseihin. Voit kokeilla niiden estimointia WREGAJK tietokoneohjelmalla. Sitä käyttäen voit lähteä liikeelle kulutus.REG tiedostosta, johon kaikkien neljän hypoteesin (Keynesin perus + kolme varianttia) mukaiset yhtälöt on jo istutettu valmiiksi.

23.3 Muut kulutukseen vaikuttavat tekijät

Tähän saakka yksityistä kulutusta on käsitelty yhtenä kokonaisuutena, mutta käytännössä se tavallisesti jaetaan vähintään kahteen komponenttiin: toisaalta kertakulutushyödykkeiden ja palvelusten ja toisaalta kestokulutushyödykkeiden kulutukseen. Tämä jako on perusteltu näiden kahden kulutuksen komponentin erilaisen luonteen vuoksi.

Erot tuloriippuvuudessa.

Kertakulutushyödykkeiden ja palvelusten kulutusta voitaisiin nimittää myös yhteisellä nimellä päivittäishyödykkeiden kulutukseksi, sillä niiden hankinta ja kulutus on jatkuva virta. Myös kestokulutushyödykkeiden kulutus voi olla jatkuvaa. Ne 'luovuttavat palveluksiaan' jatkuvasti, ehkä päivittäin, mutta niiden hankinta on jaksottaista. Ja kulutusfunktion mittaamisessa käytetyt tiedot ovat itse asiassa tietoja juuri hyödykkeiden hankinnasta, niiden ostoista. Tässä suhteessa päivittäishyödykkeet eroavat suuresti kestokulutushyödykkeistä. Ruokaa ja vaatteita on hankittava lähes päivittäin, mutta suurten kestokulutushyödykkeiden hankintaa voidaan varhentaa tai myöhentää ilman että siitä koituu suurta haittaa kulutukseen.

Kestokulutushyödykkeiden hankinnan varhentamisen ja myöhentämisen mahdollisuus näkyy niiden suurena tulojoustona verrattuna päivittäishyödykkeiden tulojoustoon. Siis riippuvuus tulomuuttujasta on erilainen. Sen vuoksi nämä kulutuksen komponentit on syytä pitää erillään. Sama asia voidaan myös ymmärtää siten, että päivittäis-hyödykkeiden kulutus etenee tasaisesti muista tekijöistä kuin tulokehityksestä riippuen, kun taas kestokulutushyödykkeiden kulutus riippuu tiukemmin tulosta ja on altis esim. suhdannevaihtelulle.

Asennetekijät.

Erityisesti kestokulutushyödykkeiden kulutuksessa voivat vaikuttaa myös erilaiset asennetekijät. Voidaan ajatella, että työttömyystilanne vaikuttaa kulutukseen paitsi suhdannetekijänä tulonmuodostuksen kautta, myös erikseen kuluttajien asenteiden kautta. Vaikutus tulonmuodostuksen kautta merkitsee yksinkertaisesti sitä, että työttömyyden kasvaessa tuotanto ja tulonmuodostus supistuvat tai kasvavat hitaammin. Siten siis ostovoiman kasvun hidastuminen tai supistuminen vaikuttavat suoraan kulutusfunktion tulomuuttujan kautta. Mutta työttömyystilanne voi vaikuttaa kuluttajien asenteisiin myös suoraan, jolloin on paikallaan sisällyttää kulutusfunktioon työttömyyttä kuvaava muuttuja myös suoraan. Mitä vaikeampi työttömyystilanne on sitä varovaisemmin kuluttajat suhtautuvat kestokulutushyödykkeiden hankintaan. Tämän mukaan on tehty AJKA mallissa. Sen kestokulutushyödykkeiden kulutusfunktiossa työttömyysmuuttuja saa tilastollisesti merkitsevän kertoimen.

Yksinkertaisesti siksi, että sama inflaatio joka nostattaa hyödykkeiden hintoja, nostattaa myös niiden ostamiseen käytettyä tuloa. Ammattiinsa perin juurin paneutunutta ekonomistia sekä kiukuttaa että naurattaa, kun ihmiset valittavat inflaatiota ja hintojen nousua. Tähän valitukseen voi useimmiten vastata: 'Mutta palkat nousevat vieläkin enemmän'. Ne nousevat täsmälleen tuottavuuden nousun verran enemmmän, sillä kaikki nousseet hinnat maksetaan viimeiseen penniin saakka tuotan-nontekijäkorvauksina, palkkoina tai elinkeinotulona tai voittoina takaisin kuluttajalle. Kuluttaja saa tulona myös niiden hyödykkeiden hinnan, jotka hän on tuottavuuden nousun ansiosta työntekijänä tai yrittäjänä tuottanut lisää.

Mutta jos tarkastellaan kulutusta komponentteihin jaettuna, voi hinnalla olla merkittävää selityskykyä. Jos esim. kulutus jaetaan päivittäiskulutukseen ja kestokulutushyödykkeisiin, voi päivittäishyödykkeiden ja kestokulutushyödykkeiden hintasuhde merkittävästi selittää kulutuksen jakautumista näiden kahden komponentin kesken. Jos päivittäishyödykkeiden hinnat nousevat enemmän kuin kestokulutushyödykkeiden hinnat, hillitään päivittäishyödykkeiden hankintaa ja lisätään suhteellisesti halvemmiksi käyneiden kestokulutushyödykkeiden hankintaa.

Liite: Koyckin muunnos

Voidaan osoittaa, että muotoa

C = a + b C1 + c Y    (2.3.1)

C = kulutus
Y = käytettävissä oleva tulo
C1 = viivästetty kulutus

oleva kulutusfunktio

• Sisältää pitkälle aikavälille jakautuneen tulomuuttujan vaikutuksen.

Koska tulomuuttujan vaikutus on pitkälle aikavälille jakautunut ja pysyväistulohypoteesin mukaan tilapäiskomponentin odotusarvo on nolla, tämä funktio on Friedmanin pysyväistulohypoteesin mukainen kulutusfunktio.

Tämän osoittamiseksi olkoon

C = a + k Y*    (2.3.2)

missä Y* on jakautunut pitkälle aikavälille taaksepäin seuraavan aritmeettisen sarjan mukaan

Y* = Y + q Y1 + q2 Y2 + ... + qn Yn    q<1    (2.3.3)

Eli tulomuuttuja Y* on yhdistelmä n edellisen kauden tuloista. Mitä aikaisemmasta tulosta on kysymys, sitä pienempi on sen merkitys (= sitä korkeampaan potenssiin sen kertoimena oleva ykköstä pienempi q korotetaan).

Hypoteesin luonteeltaan yleistävin muotoilu olisi

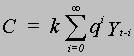
eli kulutus riippuu kaikista aikaisemmista tuloista.

Viivästetty kulutus ja tulojakauma

Oletetaan: n = 4. Silloin

C = a + k (Y + q Y1 + q2 Y2 + ... + q4 Y4) eli
C = a + k Y + kq Y1 + kq2 Y2 +...+ kq4 Y4        (2.3.4)

Pyrimme nyt osoittamaan, että viimeksi esitetty muoto on yhtä pitävä alussa esitetyn pysyväistulohypoteesin muotoilun (6.1) kanssa.

Se juuri on tarkoitus. Siihen tarvitaan

Kolme temppua plus hävittämistemppu.

Temppu 1: Viivästä kaikki termit yhdellä

C1 = a + k Y1 + kq Y2 + kq2 Y3 +...+ kq4 Y5

Temppu 2: Kerro kaikki termit tekijällä - q.

- q C1 = - qa - qk Y1 - ... - kq4 Y4 - kq5 Y5

Temppu 3: Laske yhteen (6.4) ja tempulla 2 aikaansaatu

C        = a       + k Y + kq Y1 + ... + kq4 Y4 
  - q C1 =   - q a       - kq Y1 - ... - kq4 Y4 - kq5 Y5 
--------------------------------------------------------
C - q C1 = a - q a + k Y                        - kq5 Y5 

Hävittämistemppu: unohda termi kq5 Y5

Syy:

se on niin pieni. Ja jos viiden vuoden takainen tulotermi ei ole pieni, niin ainakin esim. 25 vuoden takainen on sitä. Eli kun mennään riittävän kauas taaksepäin, tullaan pisteeseen, jossa asianomaisen vuoden tulojen vaikutus on niin vähäinen, ettei sillä ole käytännössä merkitystä.

Saadaan

• C = (1-q) a + k Y + q C1
• C = a + b Y + d C1

Nämä lausekkeet ovat selvästikin saman muotoiset.

• Molemmissa on vakiotermi, edellisessä se on tosin kahden parametrin ja vakion yhdistelmä, mutta voitaisiin yhtä hyvin korvata sijoituksella c = (1-q)a.
• Estimoinnissa saadaan joka tapauksessa vain yksi vakio.
• Molemmissa on tulotermi ja molemmissa on viivästetyn kulutuksen sisältävä termi.

Olemme siis onnistuneet osoittamaan,

• että viivästetyn kulutuksen C1 sisältämä termi sisältää itse asiassa pitkälle aikavälille taaksepäin jakautuneen tulomuuttujan Y vaikutuksen.

Koyck tietokoneohjelma

• havainnollistaa viivästetyn selitettävän kertoimen suuruuden merkitystä jakauman pituuden kannalta

Asko Korpela 980319 (971003) o Asko.Korpela@kolumbus.fi (palaute)
980319 21, 980322