22 Pääomanmuodostus [ccc]

22.1 Pääoma ja korko
F25.1 Pääomanmuodostus ja pääomakanta 1970-94
K22.1 Pääomanmuodostus Suomessa
K22.2 Pääomakanta Suomessa
o 1.1 Investoinnit maailmalla
F25.2 Pääomanmuodostus Yhdysvalloissa ja
K22.3 Pääomanmuodostuksen osuus bruttokansantuotoksesta
o 1.2 Korko ja pääomanmuodostus
22.1 Yhteenveto
22.2 Investointipäätökset
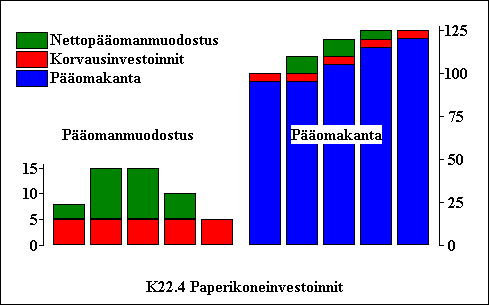
K22.4 Pääomanmuodostus Suomessa
22.3 Pääomanmuodostus ja kiihdytinperiaate
o 3.1 Tuotanto ja pääomanmuodostus
K22.5 Paperikoneinvestoinnit
o 3.2 Kiihdytinteorian matematisointi
22.4 Odotukset ja pääomakanta (joustava kiihdytin)
22.5 Pääomanmuodostus ja rahoitusmahdollisuudet
o 5.1 Nimelliskorko ja reaalikorko
oo Reaalikorko o Hallinnollinen korko
K22.6 Reaalikorko Suomessa
22.6 Pääomanmuodostus hyödykeryhmittäin

Vapaaehtoinen harjoitustehtävä: PerMakH22

Käsitteet: Reaalikorko o Hallinnollinen korko
Esimerkki: Paperin tuotanto o Taulukko: Kiihdytin o Regressiolaskelmat

Kuviot:

• F25.1 Pääomanmuodostus ja pääomakanta
• K22.1 Pääomanmuodostus Suomessa
• K22.2 Pääomakanta Suomessa
• F25.2 Pääomanmuodostus Yhdysvalloissa ja maailmalla
• K22.3 Pääomanmuodostus
• K22.4 Paperikoneinvestoinnit
• K22.5 Reaalikorko

Kyselijä:

• Mutta mikä on tämä haluttu pääomanmuodostus?
• Odotukset: eikö niistä pitänyt...
• Eikö siis Suomen kansantalouden mallin...

Tietokoneohjelmat: TreGraf o Suokok

Piirrokset: paperikone o poistot o rakennusprojekti o korkoneuvottelu o tieprojekti (Hannu Kalla)

Lähdeviitteitä o Parkin

Makron perusteet o AJK Kansantalouden kurssit o AJK kotisivu

Parkin:
[25 Investment, Capital, and Interest 593 Building the Global Village 594 Capital and Interest 595 Investment Around the World 596 Interest Pates 596 Investment Decisions 598 The Expected Profit Rate 598 The Real Interest Rate 598 investment Demand 598 investment Demand in the United States 600 ]

22.1 Pääoma ja korko

Tuotantolaitosten, koneiden ja kaluston, rakennusten ja varastojen kokonaismäärä muodostaa kansantalouden pääomavarannon. Uuden pääoman hankinta, bruttopääomanmuodostus, lisää pääomavarantoa ja olemassa olevan pääoman romuttaminen, poistot, vähentää pääomavarantoa. Pääomavaranto kasvaa nettoinvestointien määrällä. Nettoinvestoinnit ovat bruttoinvestoinnit miinus poistot (ks Chapter 23, pp. 546-547.)

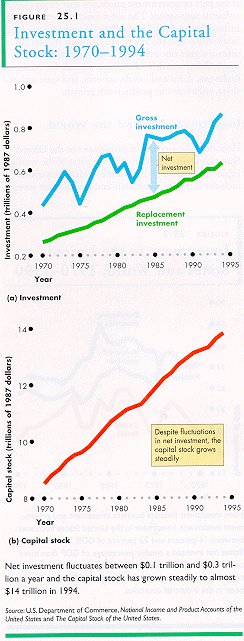
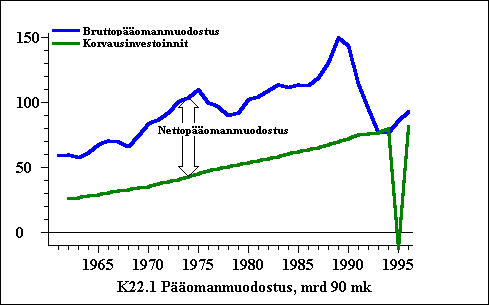
Kuviosta F25.1 nähdään pääomanmuodostus ja pääomakanta Yhdysvalloissa vuosin 1970-94. Osassa (a) nähdään, että bruttopääomanmuodostus on kasvanut ja vaihdellut. Lamavuosina se on jopa supistunut. Osa bruttopääomanmuodostuksesta korvaa kulunutta pääomakantaa. Vihreä viiva "Replacement investment" kuviossa F25.1(a) osoittaa tämän. Tämä komponentti on kasvanut, mutta siinä ei ole paljoakaan vaihtelua.

F25.1 Pääomanmuodostus ja pääomakanta 1970-94

Kuviosta F25.1 (a) nähdään myös nettoinvestoinnit eli lisäys olemassa olevaan pääomakantaan. Nettoinvestoinnit vaihtelevat kuten bruttoinvestoinnit.

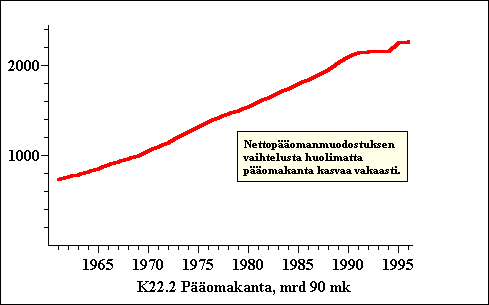
Kuviosta F25. 1 (b) nähdään kuinka pääomakanta on vaihdellut vuosittain.Pääomakannan kasvu on hidastunut laskukausina, mutta kasvu on ollut vakaata.

• Syy siihen miksi pääomakanta jatkuvasti kasvaa on, että nettoinvestoinnit ovat ollet aina positiiviset.
• Syy siihen miksi pääomakannan kasvun vaihtelu on vähäistä on, että nettoinvestointien osuus pääomakannasta on pieni.
• Kun nettoinvestoinnit laman aikana jäävät vähäisiksi, pääomakanta kasvaa noin prosentin vuosivauhdilla.
• Kun nettoinvestoinnit ovat suuret nousukautena, pääomakanta kasvaa noin 3 prosentin vuosivauhdilla. Pitkällä tähtäyksellä pääomakanta kasvaa 2 prosentin vuosivauhdilla.

Kuviosta F25.1 nähdään yksityinen pääomanmuodostus ja yksityisessä omistuksessa oleva pääomakanta.

• Yksityinen pääomanmuodostus on yritysten pääomanmuodostus plus asuntojen rakentaminen ja varastojen lisäys.
• Osa pääomanmuodostuksesta on julkista ja osa pääomakannasta kuuluu julkiselle vallalle. Kansantalouden tilinpidossa julkinen pääomanmuodostus sisältyy julkisen sektorin hankintoihin, julkiseen kysyntään. Julkista pääomanmuodostusta on se osa jolla lisätään yhteiskunnan infrastruktuuria.
• Perustavinta laatua oleva elementti yhteiskunnan infrastruktuurissa on kuitenkin lainsäädäntö ja valtiolliset elimet, jotka huolehtivat sen toteuttamisesta. Ilman tätä yhteiskunnan infrastruktuuria ei kansantaloutta olisi voitu kehittää. Muuta yhteiskunnallista infrastruktuuria ovat esim tieverkosto, vesireitit, koulut. Ne kaikki kasvattavat tuottavuuden kasvua.

K22.1 Pääomanmuodostus Suomessa

---

K22.2 Pääomakanta Suomessa

1.1 Investoinnit maailmalla

Kuviosta F25.2 nähdään investoinnit prosenttiosuuksina bruttokansantuotoksesta eri puolilla maailmaa.

F25.2 Pääomanmuodostus Yhdysvalloissa ja maailmalla

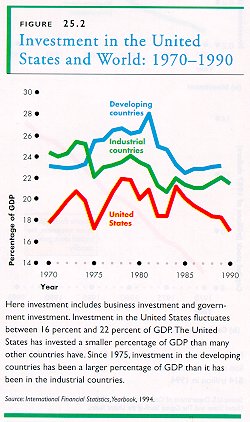Tässä pääomanmuodostus sisältää sekä yritysten että julkisen sektorin pääomanmuodostuksen. Pääomanmuodostus Yhdysvalloissa vaihtelee 16 ja 22 prosentin välillä bruttokansantuotoksesta. Yhdysvalloissa investointien osuus bruttokansantuotoksesta on alhaisempi kuin monessa muussa maassa. Vuodesta 1975 lähtien pääomanmuodostuksen osuus bruttokansantuotoksesta on ollut suurempi kehitysmaissa kuin teollisuusmaissa.

K22.3 Pääomanmuodostuksen osuus bruttokansantuotoksesta Suomessa

	Trendi aleneva kuten yllä teollisuusmaissa. Max 75 38%, min 94 17% tuotantokustannushintaisesta BKTsta. max>2*min! (WREGAJK invest)
IFAR IFAF/QGFF (osamäärä) ExpTrend: 61-95 -1,4%, 86-95 -6,4% 61-95, Sd = 0,051 61 0,360 0,353 0,331 0,334 0,353 0,359 0,346 0,318 0,332 0,350 71 0,355 0,352 0,362 0,362 0,381 0,344 0,331 0,300 0,288 0,301 81 0,303 0,306 0,308 0,292 0,289 0,282 0,285 0,300 0,326 0,310 91 0,266 0,228 0,185 0,177 0,183

1.2 Korko ja pääomanmuodostus

Pääoman tuottoa mitataan reaalikorolla. Reaalikorko on lainakorko miinus inflaatioprosentti, prosentti, jolla yleinen hintataso nousee. Esim jos korko on 10 prosenttia ja inflaatio etenee 4 prosentin vuosivauhdilla, reaalikorko on 6 prosenttia vuodessa.

Maailmalla on tuhansia erilaisia korkoja. Mutta reaalikorot kaikkialla maailmassa muuttuvat yhteydessä toisiinsa. Vuonna 1995 reaalikorko oli 6 prosentin luokkaa vuodessa. Riskipitoisissa yhteyksissä reaalikorko on korkeampi kuin riskittömissä. (Ks Reaalikorko WregAjk).

22.1 YHTEENVETO

• Nettopääomanmuodostus (bruttopääomanmuodostus miinus poistot) lisää olemassa olevaa pääomakantaa.
• Netopääomanmuodostus heilahtelee, mutta on normaalisti positiivinen, joten pääomakanta kasvaa jatkuvasti. Vaihtelu pääomakannassa on vähäistä, koska pääomanmuodostus on pieni verrattuna pääomakantaan.
• Julkisen talouden hankinnat merkitsevät lisäystä yhteiskunnan infrastruktuuriin.
• Yhdysvalloissa investointiaste (investointien prosenttiosuus bruttokansantuotoksesta) on alhaisempi kuin monissa muissa maissa, erityisesti kehitysmaissa. Pääoman tuotto on reaalikorko.

22.2 Investointipäätökset

Pääomanmuodostusta koskevaa päätöksentekoa on vaikea makrotasolla pätevästi selittää tai ennustaa, sillä

• Pääomahyödykkeiden hankintoja voidaan helposti siirtää ajassa eteen- tai taaksepäin.
• Pieni tuotannon vaihtelu voi aiheuttaa samansuuruisen muutoksen pääomakannassa, mutta moninkertaisen suhteellisen muutoksen pääomahyödykkeiden hankinnoissa.

Kulutuskysynnän riippuvuuksien ymmärtämisessä oleellinen asia oli sopivan tulokäsitteen määrittely. Lopulta päädyttiin periaatteessa kaikenkattavaan 'aikojen alusta ikuisuuteen' elinkaarihypoteesiin. Se antoi myös tilastollisesti parhaan selityskyvyn. Mutta jo vaatimattomimmallakin tulohypoteesilla päästään kohtuulliseen selityskykyyn ja, kuten myöhemmin nähdään, myös varsin hyvään ennustetarkkuuteen.

Toisin on asia pääomanmuodostuksssa.

• Ei ole olemassa mitään hyvää teoriaa, jonka avulla voitaisiin selittää yrittäjän investointipäätökiä tai pääomanmuodostusta kansantalouden kokonaisnäkökulmasta läheskään yhtä tarkasti kuin voidaan ymmärtää ja ennustaa kulutusta.
• Ei edes usean teorian yhdistelmillä päästä ennustevirheellä mitaten kuin korkeintaan puoleen siitä selityskyvystä, johon kulutuksessa päästään.

Onneksi pääomanmuodostus on bruttokansantuotoksen komponenttina korkeintaan puolet yksityisen kulutuksen suuruudesta, joten malli ei kärsi täydellistä haaksirikkoa tämän komponentin virheellisyyden takia.

• Syy pääomanmuodostuskomponentin ongelmallisuuteen on sen luonteessa.
• Pääomanmuodostusta voidaan samalla tavoin kuin kestokulutushyödykkeiden hankintoja siirtää ajassa eteenpäin tai taaksepäin kovin helposti.
• Tämän takia pääomanmuodostus voi jonakin vuonna kasvaa rajusti ja jonakin toisena taas pysyä entisen suuruisena tai jopa supistua, kun olemassa olevasta pääomakannasta poistuu loppuun käytettyjä pääomahyödykkeitä: koneita, kalustoa, rakennuksia.
• Ja kun tällaisen ruuhkautuneen pääomahyödykkeiden hankintarysäyksen aikana hankitut pääomahyödykkeet sitten kuluvat loppuun ja ne poistetaan käytöstä, sekin tapahtuu suunnilleen samanaikaisesti tietyn luonnollisen käyttöiän jälkeen.
• Näin syntyy uusi ruuhkautuma ja ruuhkautuman jälkeen suvantovaihe, koska niin suuri osa pääomakannasta on juri uusittu.
• Näin syntyy itse asiassa suhdannevaihtelu. Selvin esimerkki tästä ovat sotien jälkeiset rakennusboomit. Sota tuhoaa. Sodan jälkeen rakennetaan nopeasti uudet. Uusien rakennusten käyttöiän kuluttua tarvitaan taas uudet korvaamaan käytöstä poistetut.

IFAF Kiinteän pääoman bruttomuodostus mrd 90 mk 96026 
ExpTrend: 71-95 0.2%, 86-95 -5.9% 
61  57.4  57.8  56.0  59.3  65.7  68.3  67.4  63.9  72.1  81.0 
71  84.1  89.3  97.2 100.5 106.5  96.8  93.5  87.0  89.6  99.0 
81 101.1 105.7 109.9 107.6 110.1 109.7 115.1 126.4 145.1 139.1 
91 111.0  92.2  74.5  74.6  80.4 

22.3 Pääomanmuodostus ja kiihdytinperiaate

Avain pääomanmuodostuksen suuren vaihtelun ymmärtämiseen on kiihdytinperiaate.

Kiihdytinperiaatteen ydinajatus:

Jos tuotantokapasiteetti on täyskäytössä, pääomanmuodostusta on kasvatettava tuotannon kasvuun verrattuna kiihtyvällä nopeudella.

Tarve tuotannossa tarvittavan pääomakannan kasvattamiseen eli juuri pääomanmuodostukseen kiihtyvällä nopeudella syntyy siitä yksinkertaisesta tosiasiasta, että tietyn tuotannon määrän aikaansaamiseen tarvitaan tietyn suuruinen työpanos ja tietyt koneet, laitteet ja rakennukset eli olemassa oleva pääomahyödykkeiden varanto.

3.1 Tuotanto ja pääomanmuodostus

Pääomahyödykkeiden varannon täytyy siis olla tietyssä suhteessa tuotannon määrään. Koska pääoman muodostus on lisäystä olemassa olevaan varantoon ja vain pieni osa varannosta, sen täytyy ksvaa 'kahta kauheammin' jos varannonkin pitää kasvaa esim. 5 prosenttia sen takia, että tuotantoa on voitava kasvattaa 5 prosenttia. Tämän periaatteen on ensimmäisenä esittänyt J M Clark tutkittuaan vuosisadan alussa rautatievaunukapasiteetin kysyntää ja tarjontaa. Sama periaate voidaan esittää pelkistetyin luvuin Suomen kansantalouden ytimestä, paperiteollisuudesta kokoonkeitetyllä esimerkillä:

Näiden paperin tuotantoa koskevien tietojen perusteella laadimme yksinkertaistetun erimerkin.

• Oletamme, että 1990 konekanta on 100 kappaletta ja vuosituotanto 7 miljoonaa tonnia.
• Lisäksi oletamme, että kapasiteetti on täyskäytössä ja että paperikoneen keski-ikä on 20 vuotta, jolloin vuotuien uusimistarve on 5 konetta.
• Tällä uusintainvestointien määrällä paperikonekanta pysyy entisen suuruisena ja voidaan tuottaa jatkuvasti noin 7 miljoonaa tonnia paperia.
• Tavanomainen 3 prosentin kysynnän kasvu merkitsee, että konekantaa on myös lisättävä noin 3 prosentilla eli 3 koneella vuodessa.
• Pääomanmuodostus on siis: uusintainvestoinnit 5 plus uusinvestoinnit 3 eli yhteensä 8 konetta vuodessa.

Oletaan, että vuonna 1991 kysyntä kasvaa 10 prosenttia.

• Koska kapasiteetti on käytännöllisesti katsoen täyskäytössä, on tuotannon lisääminen mahdollista vain hankkimalla vastaavasti uusia koneita.
• Vain jos konekantaa lisätään 10 koneella, pystytään kasvanut kysyntä tyydyttämään.
• Siis investointien on kasvettava 8 asemesta 15 koneella.
• Eli 10 prosentin kysynnän kasvu aiheutti kylläkin vain 10 prosentin kasvun pääoma kannassa , mutta lähes 90 prosentin kasvun pääoman muodostuksessa .

     Kulutus Pääomanmuodostus, kpl      Koneiden 
Vuosi 1000 t korvaus netto brutto kasvu% määrä 
1990  7000       5      3      8          100 
1991  7700       5     10     15     88   110 
1992  8400       5     10     15      0   120 
1993  8750       5      5     10    -33   125 
1994  8750       5      0      5    -50   125

Jos paperin kysyntä myös vuonna 1992 kasvaa 700 tonnilla eli 10 koneen vuosituotannon verran, tarvitaan

• taaskin 5 korvausinvestointikonetta ja 10 uusinvestointikonetta eli 15 konetta.
• Nyt pääoman muodostus ei edellisestä vuodesta kasvanut lainkaan, vaikka tuotanto kasvoikin, samoin pääomakanta.
• Siis investoinnit kasvavat vain, kun tuotannon kasvu kiihtyy. Siitä nimitys kiihdytinteoria.

Tarina jatkuu edelleen.

• Jos nyt 1993 kysynnän kasvu jääkin alle puoleen entisestään, eli 350 tuhanteen tonniin, siis 5 koneen vuosituotantoon,
• investoinnit eli pääomanmuodostus supistuu 15 koneesta 10 koneeseen.
• Kysynnän kasvun pysähtyminen vuonna 1994 pudottaa edelleen investointeja, koska nyt tarvitaan vain korvausinvestoinnit eli 5 konetta.

Jo Clark korosti sitä seikkaa, että kiihdytinteoria ei toimi, jos tuotantokapasiteettia on vapaana. Silloinhan tuotantoa voidaan lisätä ottamalla käyttöön jo olemassa olevaa kapasiteettia. Mitään uusinvestointeja ei tarvita. Kiihdytinperiaate on kuitenkin kansantalouden kokonaismallissa käytettävän investointiteorian lähtökohta.

K22.4 Paperikoneinvestoinnit

3.2 Kiihdytinteorian matematisointi

Tämän, ns. naivin kiihdytinteorian matematisointi tapahtuu seuraavasti: Merkitään tuotannon määrää Q ja pääomakantaa K. Silloin pääomakerroin

k = K / Q ja K = k Q

Jos nyt tuotanto (tuotannon tarve, kysyntä) muuttuu, muuttuu pääomakannan tarve samassa suhteessa, eli

Mutta mitä on pääomakannan muutos? Mitäpä muuta kuin (netto)investoinnit eli (netto)pääomanmuodostus I_n. Investointien riippuvuus tuotannon muutoksesta voidaan siis kiihdytinteorian mukaan merkitä:

Tätä nimitetään naiviksi kiihdytinteoriaksi, yksinkertaisesti siitä syystä, ettei sillä pärjätä alkuunkaan, jos ryhdytään empiirisestä aineistosta selvittämään pääomanmuodostuksen riippuvuuksia.

• Kansantalouden kokonaistuotannon muutokset ovat käytännössä 0 ja 8 prosentin välillä. Nollakasvu edellyttäisi siis nettoinvestointien jäämistä kokonaan pois. Näin ei kuitenkaan koskaan ole tapahtunut.
• Pääoman muodostuksen kasvu on kyllä silloin tällöin ollut negatiivista, mutta koskaan nettoinvestoinnit eivät ole jääneet nollaksi, niin ei siis myöskään pääomakannan kasvu (paitsi 1995!).

Jos kuitenkin tätä periaatetta kokeillaan empiiriseen aineistoon, kuten kansion c:\ajk\kok tiedostossa INVEST.REG on tehty, kannattaa yhtälöön liittää vakiotermi, joka silloin tulkitaan autonomiseksi eli tuotannon muutoksista riippumattomaksi pääomanmuodostukseksi.

22.4 Odotukset ja pääomakanta (joustava kiihdytin)

Huomattavasti parempaan selitys- ja ennakointikykyyn päästään, jos käytetään joustavan kiihdyttimen periaatetta. Sen esittivät toisistaan riippumattomissa tutkimuksissaan Goodwin ja Chenery 1950-luvun alussa.

Lähtökohtana joustavan kiihdyttimen hypoteesissa on varannonsopeutusmalli , jonka mukaan

(Netto)pääomanmuodostus I_n tapahtuu kiinteässä suhteessa halutun pääomakannan K* ja olemassa olevan pääomakannan K1 erotukseen.

Tässä, kuten kaikkialla tässä tekstissä numero tunnisteen K1 lopussa tarkoittaa edellisen vuoden tietoa. Varannonsopeutusperiaatteen matematisointi malliksi tapahtuu seuraavasti:

I_n = m (K* - K1)

Kyllä vain. Mehän teimme sen jo. Haluttu pääomakanta on kiinteässä suhteessa haluttuun tuotantoon eli K* = k Q. Tästä saadaan taaskin (tarkkaan ottaen netto)pääomanmuodostus

I_n = m (k Q - K1)
    = m k Q - m K1

Nähdään, että tuotannon määrä on mukana kuten edellä naivin kiihdyttimen tapauksessakin, mutta nyt tuotannon taso, ei sen muutos.

Uusintainvestointien voidaan olettaa olevan poistojen suuruiset ja poistot taas tapahtuvat tietyssä suhteessa olemassa olevaan pääomakantaan. Jos poisto-osuus (= poistoprosentti/100) on d, ovat poistot (=uusintainvestoinnit)

D = d K1

Silloin bruttopääomanmuodostus on vastaavasti

I = m k Q - (m-d) K1

Kun joustavan kiihdyttimen periaatetta ryhdytään soveltamaan käytäntöön eli suoritetaan ekonometrisia laskelmia havaintoaineistolla, ei tässä saatuja kolmea parametria ole tarpeen erottaa toisistaan.

• Riittää, kun laskemme parametrit b (= m k) ja c (= - m + d).
• Käytännön laskelmiin liitämme vielä vakiotermin, joka taaskin voidaan tulkita autonomiseksi pääomanmuodostukseksi.
• Tällä tavoin joustavan kiihdyttimen hypoteesin mukainen estimoitava investointifunktio on muotoa

I = a + b Q + c K1

Oleellista on, eian mukainen malli. Selityskykyä voidaan vielä piirun verran parantaa käyttämällä yhtä 'ylimääräistä' viivettä, siis yhtälöä

I = a + b Q1 + c K2

Olikin unohtua. Tässä kehitteillä oleva kansantalouden investointifunktiolla tarkoitetaan kuvata päätöksentekoa yrityksissä samalla tavoin kuin kulutusfunktio kuvaa kuluttajien päätöksentekoa.

• Kun pääomanmuodostuksesta saadaan tilastotietoja, ne ovat tietoja toteutuneesta päätöksenteosta.
• Niitä investointeja koskevat päätökset on tehty vuotta tai paria aikaisemmin silloin vallinneen taloudellisen tilanteen mukaan.

Näin ollen kysymyksessä on ns. tekninen viive, eli se seikka, että investointipäätösten kypsyminen valmiiksi tuotannoksi vie tietyn ajan.

• Ensin päätetään ryhtyä rakennusprojektiin.
• Sitten rakennus suunitellaan, piirretään, haetaan luvat. Koosta riippuen tämä vie aikaa vähintään viikkoja, ehkä kuukausia, joskus jopa vuosia.
• Sitten tehdään perustus.
• Sitten seinät, sitten sisustus ja lopuksi viimeistellään. Nämä vaiheet eivät näy tilastotiedoissa.
• Vasta kun rakennus otetaan valmiina käyttöön, se saman tien joutuu kansantulotilaston investointeihin.

Vuosi sitten vallinneita odotuksia kuvaa viimeksi kehittelemässämme investointifunktiossa silloin vallinnut taloudellinen tilanne. Viimeksi käsittelemässämme joustavan kiihdyttimen hypoteesissa odotuksia kuvaavat siis vuoden takainen eli yhdellä viivästetty tuotannon määrä ja kahdella viivästetty eli päätöshetkeä edeltäneen vuoden pääomakanta.

22.5 Pääomanmuodostus ja rahoitusmahdollisuudet

Markkinakoron tehtävä

Suomen kansantaloudessa on pitkään vallinnut tilanne, jossa korolla ei ollut sitä resursseja ohjaavaa tehtävää, jota tässäkin taustalla käytetty bruttokansantuotoksen ja koron samanaikaista tasapainottumista edellyttävä ISLM malli kuvaa.

• Vasta viime vuosina tilanne Suomessa on muuttunut ja korko on saanut entistä huomattavasti tärkeämmän merkityksen yritysten investointipäätöksistä.
• Vasta tässä tekstissä, 16 vuotta AJKA mallin syntymisen jälkeen, on ensi kerran voitu ottaa tarkasteltavaksi pääomanmuodostuksen riippuvuus korkotasosta niin että havaintaineistosta estimoitu malli saa odotusten mukaiset parametrien etumerkit ja sekä selitysaste että t-arvot täyttävät niitä koskevat minimivaatimukset.
• Tästä syystä myöskään tämän tekstin taustana olevassa Suomen kansantalouden AJKA mallissa ei ole ollut eikä ole vieläkään rahoitusmarkkinalohkoa.

On kyllä. Suomen Pankissa on jo 1960-luvulla tehty pioneerityö Suomen kansantalouden mallien rakentamisessa ja siinä yhteydessä kehitettiin erilaisia vaihtoehtoisia indikaattoreita, joilla kuvattiin rahoitusmarkkinoiden kireyden vaikutusta pääomanmuodostukseen.

Suomen Pankin BOF1 mallissa luoton saatavuuden mittarina käytettiin pankkien keskuspankkiluoton suhdetta pankkien luotonantoon yksityiselle sektorille. AJKA mallissa on käytetty vastaavasti keskuspankkiluoton suhdetta talletuksiin.

Rahoituksen kannalta tarkasteltuna korko on rahan hinta, korvaus joka on maksettava rahan käyttöoikeudesta.

• Jos käytetään omaa rahaa, on korko silloinkin rahan käytön kustannus, sillä se saataisiin, jos oma raha annettaisiin markkinoiden käyttöön.
• Tällaista laskennallista kustannusta nimitetään vaihtoehtoiskustannukseksi .

5.1 Nimelliskorko ja reaalikorko

Ennenkuin otetaan korko rahoituksen saatavuuden kuvaajaksi investointifunktioon, on tehtävä eräs tärkeä tarkennus. On erotettava toisistaan käsitteet nimelliskorko ja reaalikorko.

• Markkinoilla normaalisti muodostuva korko on nimelliskorko. Jos korkoa ajatellaan investointihyödykkeen rahoituksen kustannuksena, niin investointihyödykkeellä aikaansaatavan tuotannon 'normaali' hinnannousu tekee mahdolliseksi maksaa osan korkokustannuksista ikäänkuin ilmaiseksi.
• Vasta se osa korkokustannuksesta, jota inflaatio ei kata, on investoinnin maksettava reaalisella tuottavuudellaan. Tämä osa korosta on reaalikorko.

Reaalikorko

on nimelliskorko (markkinakorko, tässä pankkien antolainauskorko) vähennettynä inflaatioprosentilla.

K22.6 Nimelliskorko ja reaalikorko

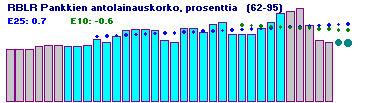RBLR Pankkien antolainauskorko prosenttia BF3.4.5 ExpTrend: 62-95 1.2%, 86-95 -0.6% 62-95, Sd = 1.5 61 7.0 7.0 7.0 7.0 7.4 7.5 7.5 7.4 7.4 7.5 71 8.4 7.9 8.7 9.5 9.7 9.7 9.5 8.2 8.0 9.8 81 9.8 9.3 10.4 10.7 9.0 9.0 9.0 9.9 10.6 11.8 91 12.1 12.5 10.2 8.2 8.0

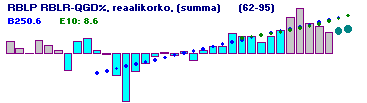RBLP RBLR-QGD%, reaalikorko (summa) LinTrend: 62-95 0.2, 86-95 0.5 62-95, Sd = 4.6 61 7.0 3.1 1.3 -0.1 3.2 1.9 0.7 -4.7 3.0 3.9 71 0.8 -0.3 -5.9 -12.9 -5.0 -2.8 -0.8 0.1 -0.6 0.4 81 -2.0 0.7 1.8 1.8 5.2 4.4 4.3 2.8 4.5 6.0 91 9.6 11.8 7.8 7.0 5.4

Kuviot talletettu leikepöydälle Wregajk muunnosmenusta. Leikepöydältä kuviot on siirretty kuvankäsitteluohjelmaan, jossa ne on tallennettu HTML kielen vaatimaan .GIF muotoon.

Hallinnollinen korko

Suomessa aina 80 luvun puoliväliin saakka rahoitusmarkkinoilla ei näytellyt pääosaa sen enempää nimelliskorko kuin reaalikorkokaan, vaan kolmas korkokanta eli hallinnollinen korkokanta. Se on se korkokanta, joka näkyy havaintosarjana, esim. AJKA mallissa käytettynä pankkien antolainauskorkona. Hallinnollista korkokantaa ylläpidettiin hallinnollisin toimenpitein.

Oleellista on, että hallinnollinen korkokanta pidettiin normaalin kysynnän ja tarjonnan edellyttämän markkinakoron alapuolella. Tämä korko jouduttiin lainarahoituksesta maksamaan. Siinä mielessä

• hallinnollinen korko oli myös markkinakorko. Mutta tästäkin 'luonnollista' alemmasta korosta inflaatio maksoi täysimääräisesti osuutensa.
• Jäljelle jäi reaalikorko, joka nopeimman inflaation vuosina eli melkein koko 70 luvun ajan oli negatiivinen ja hyvin alhainen aina siihen saakka, kun inflaatio taintui.
• Tämä taas merkitsi sitä, että melkein mikä hyvänsä investointi oli riittävän tuottava rahoituksen korkokustannuksen maksamiseksi.

Tästä taas seurasi, että

• korko ei suorittanut tehtäväänsä resurssien allokoinnissa eli hyvien ja huonojen investointiprojektien erottamisessa toisistaan.
• Tämä ongelma oli ratkaistava muilla keinoilla. Alkuun rahoitus ohjautui kohteisiinsa 'hyvien pankkisuhteiden' avulla.
• Myöhemmin pankit, jouduttuaan karvaasti kokemaan tämän allokaattorin puuttellisuuden, kehittivät mittavan yritystutkimustoiminnan, jonka tehtävä oli erottaa jyvät akanoista.
• Jos taas korko on todellinen ja merkittävä rahoituksen kustannus se toimii myös allokaattorina, ja yritykset joutuvat itse punnitsemaan investointiprojektinsa tuottavuuden.

Ydinajatus kaikissa rahoituksen saatavuutta koskevissa hypoteeseissa on

• vastakkainasettelu investoinnin rajatehokkuuden ja rahoituksen rajakustannuksen välillä.
• Tässä on täydellinen analogia tavanomaiseen markkinahinnan määräytymiseen kysynnän ja tarjonnan vuorovaikutuksessa.
• Jos investointiprojektit asetetaan niiden tuottavuuden mukaan paremmuusjärjestykseen, saadaan korkoakselin ja investointien määrän muodostamaan koordinaatistoon alaspäin viettävä käyrä. Se vastaa kysyntäkäyrää hinta- ja määräakselien muodostamassa koordinaatistossa.
• Vastaavasti rahoituksen kustannukset ovat kasvava funktio rahoitettavien projektien määrän suhteen korko-määrä-akselistossa.
• Mitä enemmän halutaan investoida sitä riskipitoisempia projekteja joudutaan toteuttamaan ja sitä korkeampi on oltava korkokorvaus niiden rahoittajalle.
• Toteutuva korkotaso on se, jolla rahoituksen korko-kustannus (rahoituksen rajakustannus) on yhtä suuri kuin investoinnin korkotuotto (rajatehokkuus).

22.6 Pääomanmuodostus hyödykeryhmittäin

AJKA mallissa pääomanmuodostus on käsitelty yhtenä eränä. Näin on tehty kahdesta syystä: koko pääomanmuodostus on alle puolet yksityisen kulutuksen suuruudesta. Disaggregointi ei tuo oleellista parannusta mallin suorituskykyyn kokonaisuutena. Pantiinpa pääomanmuodostus malliin miten hyvänsä, se on ja pysyy eräänä kansantalouden mallin heikoimmista lenkeistä selityskykynsä ja ennakointikykynsä suhteen.

Periaatteessa kuitenkin pääomanmuodostus jakaantuu sitä koskevan päätöksenteon kannalta tarkasteltuna luontevasti hyvin erilaisiin komponentteihin:

• Asuntojen rakentaminen tyydyttää yksityistä kulutuskysyntää ja sen rahoituksessa yksityisen sektorin säästämisellä on suuri merkitys.
• Tuotannollinen pääomanmuodostus, muu kuin auntorakentaminen, kone- ja laiteinvestoinnit, tapahtuu yritysten toimesta ja liittyy kiinteästi tuotantotoimintaan.
• Tie- ja vesirakennusinvestoinnit ovat nekin oma lukunsa ja tapahtuvat suurimmaksi osaksi yhteiskunnan toimesta. Niiden tarkoituksena on usein tasoittaa suhdannevaihtelua, jota taas kaikki muut pääomanmuodostuksen lajit ovat ensimmäisenä aiheuttamassa.

nyt muutamiin pääomanmuodostusta koskeviin hypoteeseihin voit kokeilla niiden estimointia WREGAJK tietokoneohjelmalla. Se lähtee liikeelle INVEST.REG tiedostosta, johon tässä käsitellyt naivin kiihdyttimen ja joustavan kiihdyttimen hypoteesien mukaiset yhtälöt on jo istutettu valmiiksi.

Lähdeviitteitä:

J.M. Clark:

Business Acceleration and the Law of Demand, Journal of Political Economy, Vol. 25, No 1 (March, 1917), pp. 217-35.

R.M. Goodwin:

"The Non-linear Accelerator and the Persistence of business Cycles", Econometrica, Vol. 19, No 1 (Jan 1951), pp. 1-17.

H.B. Chenery:

"Overcapacity and the Acceleration Principle", Econometrica, Vol 20, No 1 (Jan 1952), pp. 1-28.

Kukkonen et al.

A Quarterly Model of the Finnish Economy, Bank of Finland D:29, Helsinki 1972.

Korpela Asko

AJKA, an Econometric Model for Finland, Helsinki School of Economics A:36, Helsinki 1982.

Hicks J.R.

ISLM mallissa I = investoinnit, S = säästäminen - hyödykemarkkinoiden tasapaino.
L = rahan (likviditeetin) kysyntä, M = rahan tarjonta - rahamarkkinoiden tasapaino.

'Mr. Keynes and the Classics: A Suggested interpretation,' Econometrica 1937, pp. 147-159.

Asko Korpela 980317 (980126) o Asko.Korpela@kolumbus.fi (palaute) [ccc]