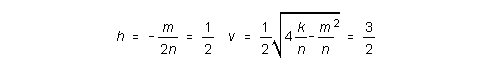
H17 Markkinamalli ja hintaodotukset 31D020

Odotukset
1. Oletetaan kysyntä ja tarjonta
2. Oletetaan kysyntä ja tarjonta
3. Osoita, että (m/n)2 < 4 (k/n) tapauksessa n ja
4. Selvitä karakteristiset juuret ratkaisematta

Odotukset

Q_d = j₁ + k₁ P + m₁ P' + n₁ P'' (j₁>0, k₁<0)

Q_s = j₂ + k₂ P + m₂ P' + n₂ P'' (j₂>0, k₂<0)

1. Oletetaan kysyntä ja tarjonta

Q_d = 10 - 2 P + 3 P' - P''

Q_s = - 5 + 3 P - 7 P' + 4 P''

Alkuehdot: P(0) = 5 ja P'(0) = 3

a) Selvitä aikaura P(t) .

b) Mikä on tasapainohinta ?

c) Suppeneeko aikaura? Mikä on dynamiikan luonne?

Vastaus:

y''(t) + a₁ y'(t) + a₂ y = b (15.2)

a) Tässä:j = 15 k = - 5 m = 10 n = - 5

a₁ = m/n = - 2 a₂ = k/n = 1 b = - j/n = 3

Näistä saadaan: a₁² = (m/n)² = 4 = 4 (k/n) = 4 a₂

kaksoisjuuri: r = - a₁/2 = - m/(2 n) = 1

Erityisratkaisu: P_p = b/a₂ = - j/k = 3

Täydellisen yhtälön yleinen ratkaisu:

P(t) = A₃ e^t + A₄ t e^t + 3

Alkuehtojen perusteella:

P(0) = A₃ + A₄ 0 1 + 3 = 5 A₃ = 2

P'(t) = A₃ e^t + A₄ e^t + A₄ t e^t

P'(0) = 2 + A₄ = 3 A₄ = 1

P(t) = 2 e^t + t e^t + 3

b) Markkinamallin tasapaino: = 3

c) Ei suppene tasapainoon: r = 1 > 0 räjähtää aaltoilematta

2. Oletetaan kysyntä ja tarjonta

Q_d = 9 - P + P' + 3 P''

Q_s = - 1 + 4 P - P' + 5 P''

Alkuehdot: P(0) = 4 ja P'(0) = 4

a) Selvitä aikaura P(t) .

b) Mikä on tasapainohinta ?

c) Suppeneeko aikaura? Mikä on heilahtelun luonne?

Vastaus:

a) Tässä: j = 10 k = - 5 m = 2 n = - 2

a₁ = m/n = - 1 a₂ = k/n = 5/2 = 2.5 b = - j/n = 5

Näistä saadaan: a₁² = (m/n)² = 1 < 10 = 4 (k/n) = 4 a₂

kompleksijuuret: r₁,r₂ = h ± vi

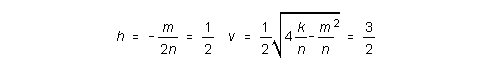
Erityisratkaisu: P_p = b/a₂ = - j/k = 2

Täydellisen yhtälön yleinen ratkaisu:

P(t) = e^t/2 ( cos (3t/2) + sin (3t/2)) + 2

Alkuehtojen perusteella:

P(0) = + 2 = 4 = 2

P'(t) = (1/2) e^t/2 ( cos (3t/2) + sin (3t/2))

+ e^t/2 (- (3/2) sin (3t/2) + (3/2) cos (3t/2))

P'(0) = (1/2) (2 + 0) + (0 + (3/2) ) = 4 = 2

P(t) = e^t/2 (2 cos (3t/2) + 2 sin (3t/2)) + 2

b) Markkinamallin tasapaino: = 2

c) Ei suppene tasapainoon: h = 1/2 > 0 räjähtää aaltoillen.

3. Osoita, että (m/n)² < 4 (k/n) tapauksessa n ja m on oltava samanmerkkiset, jotta tasapainoon päästäisiin.

Vastaus:

Tässä kompleksijuuritapauksessa konvergenssi vaatii, että reaaliosa h on negatiivinen. Koska h = - m/(2 n), h on negatiivinen vain jos n ja m ovat samanmerkkiset.

4. Selvitä karakteristiset juuret ratkaisematta seuraavia yhtälöitä. Päättele juurista suppeneminen.

a) P'' + 3 P' + 2 P = 4 b) P'' - 2 P' - 3 P = - 8

c) P'' - 4 P' + 4 P = 9 d) P'' + 2 P' + 5 P = 3

e) P'' - 3 P' + 10 P = 7 f) P'' + 5 P' + 8 P = 10

Vastaus:

a) molemmat negat, konvergointi

b) r₁,r₂ = 3, - 1 toinen positiivinen, divergointi

c) r₁ = r₂ = 2 posit kaksoisjuuri, divergointi

d) reaaliosa negat, konvergointi

e) reaaliosa posit, divergointi

f) reaaliosa negat, konvergointi

Asko Korpela 971111 (971111) o Asko.Korpela@kolumbus.fi (palaute)

[ccc]